Bayesian parameter inference for simulation-based models
Many applications in science and engineering use stochastic numerical simulators to understand a phenomenon of interest. Such a simulator can be given, e.g., as a set of differential equations derived from first principles, as a phenomenological model, or simply as a computer program $f(\cdot)$ that takes as input a set of parameters (of interest) $\theta$ and produces a set of simulated data $x$:
$$ f: \theta \mapsto x. $$
The primary challenge in working with simulation-based models is finding the parameter settings that accurately replicate observed data $x_o$. A straightforward solution might be to search for the single best-fitting parameter settings $\theta^*$ using grid search or standard optimization algorithms. However, this approach often falls short in high-dimensional problems and complicates the identification of multiple valid parameter settings, the expression of parameter uncertainties, and the description of parameter interactions, which are all valuable properties when working with scientific simulators.
A more principled approach is given by Bayesian parameter inference. Rather than obtaining single-point estimates, Bayesian inference aims to obtain a distribution over model parameters conditioned on the observed data, $p(\theta \mid x_o)$. This so-called posterior distribution characterizes the entire parameter space, highlighting regions likely to reproduce observed data. It thereby identifies all possible parameter settings likely to explain the observed data and quantifies parameter uncertainties and correlations.
More formally, given a prior $p(\theta)$ characterizing our prior knowledge about the parameters, and a likelihood $p(x \mid \theta)$ defined by the simulation-based model, Bayesian inference aims to infer the posterior over the parameters via Bayes’ rule:
$$ p(\theta \mid x) = \frac{p(x \mid \theta)p(\theta)}{p(x)}. $$
Simulation-based inference (SBI)
Simulation-based inference (SBI) aims to facilitate Bayesian parameter inference for simulation-based models. The central challenge for SBI arises from the complexity of scientific simulators, where computing the likelihood $p(x \mid \theta)$ is difficult because the simulator $f(\theta)$ acts like a black box: It allows us to simulate data, that is, to sample from the likelihood, but we cannot explicitly determine or write down an expression for its likelihood. Consequently, standard approximate Bayesian inference methods such as Markov Chain Monte Carlo (MCMC) or Variational Inference (VI) are not applicable as they necessitate efficient access to the model’s likelihood $p(x\mid\theta)$. Thus, the central goal of SBI is to approximate the posterior distribution over model parameters $p(\theta \mid x_o)$ using only simulated data $(\theta, x)$ and without requiring explicit access to the model’s likelihood (Figure 1).
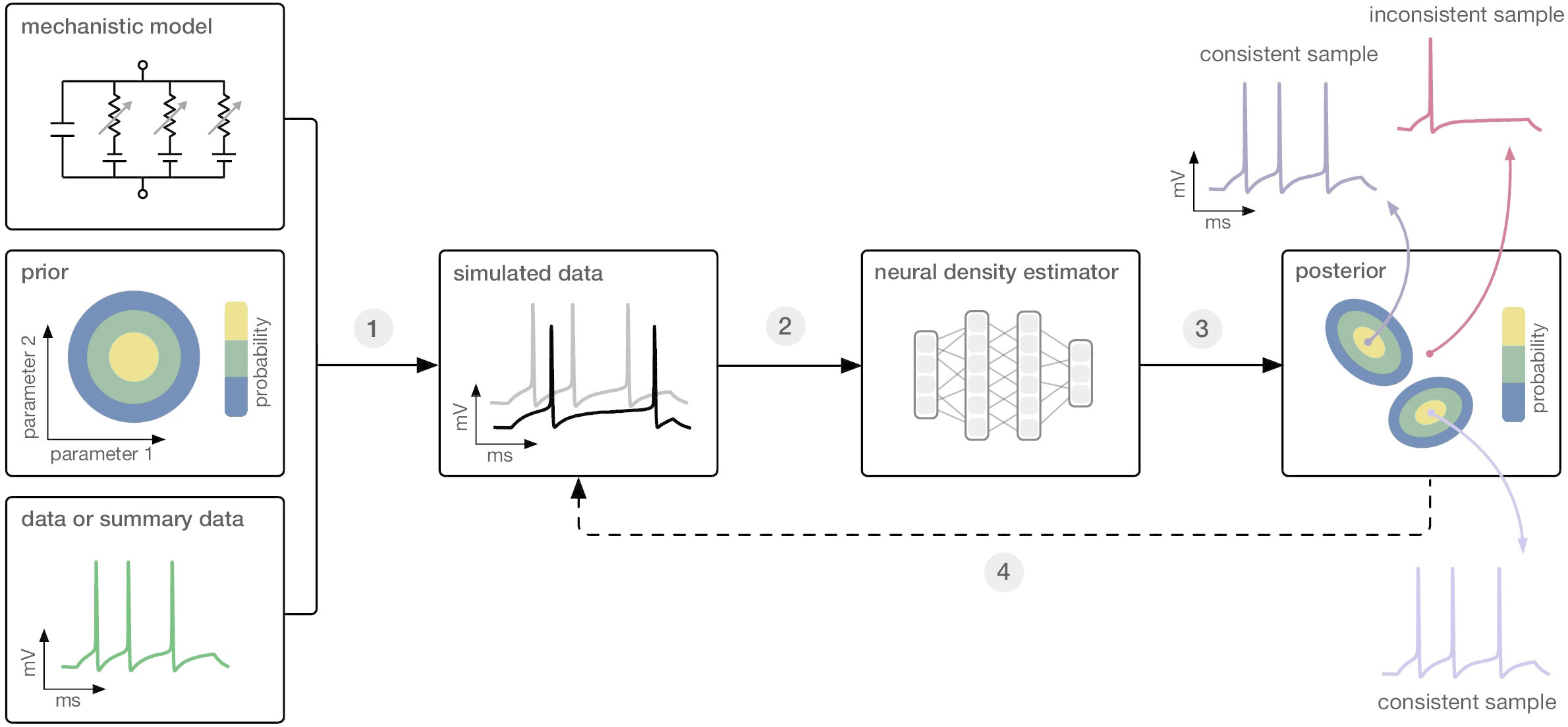
Figure 1: [Gon20T] Figure 1, Simulation-based inference: Given a simulation-based model, a prior over model parameters and observed data, SBI enables Bayesian parameter inference using only simulated data, i.e., without explicitly evaluating the likelihood of the simulator.
A primary constraint of SBI methods is that simulations are often computationally intensive. Therefore, the various SBI methods primarily differ in their efficiency in using simulated data. These methods can be divided into two categories. The first one includes classical SBI approaches based on rejection sampling, also known as Approximate Bayesian Computation (ABC, [Sis18H]). The second category comprises more recent SBI approaches that utilize artificial neural networks, which we refer to as neural simulation-based inference [Cra20F].
Classical SBI: Approximate Bayesian Computation
The practice of performing Bayesian parameter inference for intractable simulation-based models has its roots in the 1980s [Rub84B]. The idea was to offset the lack of access to the likelihood by using simulated data, and to approximate the posterior through rejection sampling. This process involves defining a distance function between simulated and observed data, $d(x, x_o)$, simulating data $x_i$ using parameters $\theta_i$ sampled from the prior, and accepting or rejecting $\theta_i$ based on a threshold parameter $\epsilon$ on the distance: $d(x, x_o)<\epsilon$. The distribution of accepted parameters
$$ q_{\epsilon}(\theta \mid d(x, x_o) < \epsilon) $$
then converges to the true posterior distribution as the amount of simulated data approaches infinity and $\epsilon$ approaches 0.
Rejection sampling methods for SBI are commonly known as Approximate Bayesian Computation (ABC). However, ABC encounters challenges with the curse of dimensionality: as the dimensionality of model parameters or data increases, the number of required model simulations for an accurate posterior estimate grows exponentially. Although there have been efforts to extend the basic rejection sampling algorithm to enhance sampling efficiency, particularly through sequential Monte Carlo variants, scaling these methods to high-dimensional problems remains difficult. Additionally, ABC methods typically necessitate ad-hoc choices of distance functions, rejection thresholds, and summary statistics. Recent advancements in neural network-based density estimation methods have partially addressed these constraints, leading to the emergence of neural network-based SBI methods.
Modern SBI: neural density estimation
The main idea of neural SBI approaches is to use artificial neural networks to learn a parametric approximation to the unknown posterior distribution $p(\theta \mid x_o)$. The neural network is trained using only simulated data, i.e., given a simulation-based model, $f$, and a prior distribution over simulation parameters $p(\theta)$, one generates the training data set ${(\theta_i, x_i)}$ simply by sampling from the prior and simulating data $x_i \sim f(\theta_i)$. Then, after training, the network is applied to the observed data $x_o$ to obtain the desired posterior approximation.
Figure 2. [Lue21B] Figure 1: Overview of SBI methods: Rejection sampling-based approaches (Monte Carlo ABC) obtain approximate posterior samples by comparing simulated and observed data. In contrast, modern SBI methods use artificial neural networks to estimate the likelihood, the posterior, or a ratio from simulated data and subsequently evaluate the trained estimator on observed data.
Current neural SBI methods can be divided into three categories based on whether they directly approximate the posterior distribution, the likelihood, or a ratio of likelihoods (Figure 2). Each approach has its strengths and weaknesses depending on the specific SBI problem. However, they all share a common advantage over traditional ABC methods: they learn a function in the data or parameter space, which allows them to leverage the capabilities of neural networks to learn embeddings and interpolations in that space, resulting in significantly improved data efficiency [Lue21B].
Neural posterior estimation
Neural Posterior Estimation (NPE, [Pap18F]) aims to directly approximate the posterior from simulated data. It uses a training dataset ${ (\theta_i, x_i) : i = 1, \ldots, N }$ to train an amortized conditional neural density estimator to approximate the posterior over the model parameters $q_{\phi}(\theta \mid x) \approx p(\theta \mid x)$. Here, $q_{\phi}$ is parameterized by a neural network with parameters $\phi$, taking $x$ as input and outputting a density in $\theta$.
Initially, NPE utilized mixture density networks, such as a mixture of Gaussian [Pap18F] and later normalizing flows [Gre19A] as conditional density estimators. The neural network parameters are optimized by minimizing the negative log-posterior density under the current estimate of the posterior:
$$ \mathcal{L}(\phi) = - \frac{1}{N} \sum_{i=1}^N \log q_{\phi} (\theta_i \mid x_i). $$
However, any conditional density estimator can be used for NPE. Recently, new versions of NPE have been introduced: neural posterior score estimation (NPSE) uses score-matching (or diffusion) networks [Sha22S, Gef23C] and flow matching posterior estimation (FMPE) uses continuous normalizing flows via flow matching [Wil23F].
A key feature of NPE is that after training it once with simulated data, it enables fully amortized Bayesian inference: obtaining posterior estimates for new observed $x_o$ requires a single forward pass in the neural network. Moreover, NPE can handle high-dimensional structured data, like time series or image data, by training it end-to-end with an appropriate embedding network attached to the density estimator.
Neural likelihood estimation
Neural Likelihood Estimation (NLE, [Pap19S]) shares similarities with NPE, but it focuses on approximating the likelihood $p(x \mid \theta)$ rather than the posterior. The conditional density estimator $q_{\phi}$ could be the same as in NPE, but it is trained to map simulation parameters $\theta$ to data $x$, thereby emulating the simulator: $x \sim q_{\phi}(x \mid \theta) \approx f(\theta)$.
Once trained, the neural likelihood $q_{\phi}(x \mid \theta)$ offers a tractable density that can be evaluated and sampled from, superseding the intractable simulator. This allows us to use standard approximate Bayesian inference methods for SBI, e.g. MCMC or Variational Inference (VI, [Glo22V]).
NLE’s key feature is its ability to emulate the simulator. Post-training, it can generate synthetic data using a single forward pass through the neural network, often faster than simulating data. It also supports efficient and flexible changing of hierarchical inference settings, e.g. when dealing with independently and identically distributed (iid) data often used in trial-based experiments under varying conditions [Boe22F].
However, NLE has its challenges. It is difficult to use with high-dimensional data $x$ as it does not support learning embeddings in $x$ but requires learning a full density in $x$. It does, however, support learning embeddings for $\theta$. Furthermore, NLE is only partially amortized: while the neural network is trained only once, inference via MCMC and VI must be repeated for each new observation $x_o$, which can be computationally and algorithmically demanding.
Neural ratio estimation
Neural Ratio Estimation (NRE, [Her20L]) trains a neural network to predict the likelihood-to-evidence ratio for a given parameter. The learned ratio estimator then enables standard Bayesian inference methods like MCMC. Consequently, NRE shares some characteristics with NLE: It allows for flexible inference in hierarchical settings with iid-data, but it’s only partially amortized, necessitating a new MCMC run for each new observation $x_o$.
Unlike NLE and NPE, NRE does not perform conditional density estimation. Instead, it treats the task of learning a density ratio as a classification problem. The aim is to train a classifier that inputs parameters $\theta$ and data $x$ and predicts the corresponding likelihood-to-evidence ratio. This approach enables learning embeddings for both $\theta$ and $x$.
All-in-one simulation based inference
Recently, a new SBI algorithm has been proposed [Glo24A] that is trained on the joint distribution of parameters and data $p(\theta, x)$ and allows to perform inference given arbitrary conditionals of the joint, including but not limited to the posterior and the likelihood. This so-called Simformer combines a transformer architecture combined with denoising score-matching. On the benchmarks presented in the paper, it clearly outperformed NPE in terms of posterior accuracy and simulation efficiency. See [Glo24A] and our paper pill for details.
Resources
The website simulation-based-inference.org serves as an introduction to SBI, providing an overview of the various applications of SBI and tracking SBI-related research papers. Similarly, the GitHub repository awesome-neural-sbi compiles information about SBI software, methods, and their applications. Additionally, the TransferLab offers a comprehensive course on SBI.
Several software packages are available for applying SBI:
- sbi implements most of the recent amortized and sequential neural network-based SBI algorithms. It has gained adoption among SBI researchers and practitioners across different domains. The package is actively maintained by developers from the community and offers extensive documentation and beginner-friendly tutorials.
- Lampe Lampe focuses on amortized neural posterior and neural ratio estimation. It provides a low-level API, making it convenient to customize existing approaches.
- swyft implements truncated marginal neural ratio estimation (TMNRE) [Mil21T], a highly simulation-efficient method commonly used for SBI problems in astrophysics.
- BayesFlow BayesFlow implements amortized NPE and (NLE), different embedding network architectures, model comparison methods, and methods for detecting model misspecification.
- pyabc implements sequential Monte Carlo ABC (ABC-SMC) methods, focusing on parallelization and distributed cluster setups.
Challenges
Limited training data and large parameter spaces
A significant challenge in SBI is the limited training data due to the high computational demand of simulations. This makes SBI application difficult in scenarios with high-dimensional parameter spaces and uninformed (e.g. uniform) prior distributions. A strategy to mitigate this is to perform multiple rounds of neural network training, generating new training data not from the prior, but from a suitable proposal distribution, such as the current posterior estimate $p(\theta \mid x_o)$. Intuitively, this approach focuses the generation of training data on parameter space regions most informative about $x_o$, facilitating more efficient parameter space exploration.
This sequential inference approach can be applied to NPE, NLE, and NRE, resulting in their sequential variants: SNPE, SNLE, and SNRE. A systematic benchmark study showed these sequential variants require less training data than single-round inference using training data from the prior [Lue21B].
However, the data efficiency improvement from multi-round inference comes with trade-offs. It requires retraining for each new observation $x_o$ and can lead to numerical instabilities, particularly for NPE, necessitating additional algorithmic adjustments [Pap18F, Gre19A]. Additionally, for NLE and NRE, sampling new training data from the proposal distribution via methods like MCMC or VI is typically slower than sampling from the prior.
A promising approach to enhance the data efficiency of SBI methods while avoiding additional algorithmic challenges is the development of more effective density estimators. For instance, recent breakthroughs like using flow matching for efficient and scalable training of continuous normalizing flows [Lip22F] have demonstrated impressive results on a set of benchmark tasks for SBI [Wil23F]. These advancements hold great promise for enabling more robust applications of SBI across diverse domains.
Learning summary statistics with embedding networks
In real-world scenarios, data generated by simulation-based models can vary widely, spanning from simple scalar observations to complex datasets such as multiple time series or cosmological and medical imaging data. Consequently, a significant challenge in applying SBI lies in extracting relevant features and reducing data dimensionality for efficient processing by SBI methods. While in some cases, hand-crafted summary statistics can be derived from high-dimensional data using expert domain knowledge, neural network-based SBI approaches like NPE or NRE offer a more general advantage: the capability to automatically learn embedding networks. This feature significantly simplifies the process of feature extraction and dimensionality reduction.
For instance, when working with image data, convolutional embedding networks are typically chosen [Gre19A, Ram22G], while sequential data like time series or text often calls for recurrent neural networks or a transformer architecture [Lue17F, Sch23C]. For trial-based i.i.d. data, permutation invariant embeddings are employed [Rad22B]. These decisions typically rely on domain-specific expertise that is separate from the selection of the SBI method.
Posterior accuracy
Theoretically, the approximations to the posterior, likelihood, or likelihood-evidence ratio are guaranteed to be accurate in the infinite data and infinite density estimator capacity regime. However, practical limitations, such as finite training data, can lead to inaccuracies, sparking recent discussions in SBI research regarding potential overconfidence in obtained posteriors [Her23C]. Various techniques have emerged to detect and mitigate these inaccuracies and biases without direct access to the underlying posterior.
- Posterior predictive checks test whether data simulated with parameters sampled from the posterior actually reproduce the observed data $x_o$.
- Simulation-based calibration (SBC) [Tal20V] and multi-dimensional coverage diagnostics [Dei22T, Can22I] use simulated data to evaluate the statistical calibration of posterior uncertainties.
- Balanced neural ratio estimation (BNRE) [Del22R] introduces a regularized loss function that allows for balancing posterior accuracy against potential overconfidence.
Additionally, posterior approximation is often not the final goal but an intermediate step to estimate the parameter’s uncertainty. The derived uncertainties can be used for downstream tasks like Bayesian decision-making [Gor23A]. In these cases, the accuracy of the posterior approximation is crucial for the result of the downstream task.
Model misspecification
When using SBI methods for inferring model parameters, it is typically assumed that the model is well-specified, i.e., capable of reproducing the observed data $x_o$. Deviations from this assumption can lead to substantially biased posterior estimates, especially with neural network-based SBI methods [Can22I].
One approach to assess model misspecification is conducting a prior predictive check, which evaluates whether the simulated data closely resembles the observed data $x_o$. Recently, automated techniques have been introduced to detect model misspecification in SBI [Sch22D]. Furthermore, new SBI methodologies have emerged, which either detect and compensate for model misspecification by learning an error model atop the simulator [War22R] or mitigate it during the inference process [Gao23G] using the generalized Bayesian inference framework [Bis16G].
Related to the problem of model misspecification is the issue of adversarial attacks. On the one hand, adversarial attacks can be used to assess how susceptible an SBI method is to small worst-case perturbations in the data, e.g. to study robustness to model misspecification. On the other hand, as the application of SBI methods extends into safety-critical scientific and industrial fields, the significance of real-world attack scenarios grows. [Glo23A] recently tackled this issue by introducing a variant of NPE that exhibits greater resilience to adversarial attacks than conventional neural SBI methods.
Outlook
The field of Simulation-Based Inference (SBI) is poised for significant advancements, particularly with the recent advances in neural network-based methods. These advancements offer promising avenues for enhancing scientific model building across various disciplines. By leveraging neural networks, SBI methods can more effectively handle complex and high-dimensional models, leading to more accurate and efficient inference processes. This not only enables researchers to better understand and refine their models but also holds potential applications in industrial contexts, where precise modeling and prediction are critical for optimizing processes and improving outcomes. As these neural network-based SBI methods continue to evolve, bridging the gap between methodological advancements and the development of accessible software tools and guidelines for practitioners remains a significant challenge.

