Recent developments in simulation-based inference (SBI) have mainly focused on parameter estimation by approximating either the posterior distribution or the likelihood. The general idea is to use samples from the prior distribution and corresponding simulated data to train neural networks that learn a density in the parameters (for posterior estimation) or a density in the data (for likelihood estimation). Successful applications of this approach employed normalizing flows [Pap19S], score matching [Sha22S], or flow matching [Wil23F] (covered in our recent pills).
The Simformer
All-in-one simulation-based inference [Glo24A] takes a different approach. It uses a transformer architecture that is trained on the joint distribution $p(\theta, x) =: p(\hat{x})$, taking both parameters and data as input. It thereby encodes parameters and data and predicts the score function to perform inference via score-based diffusion models [Son19G].
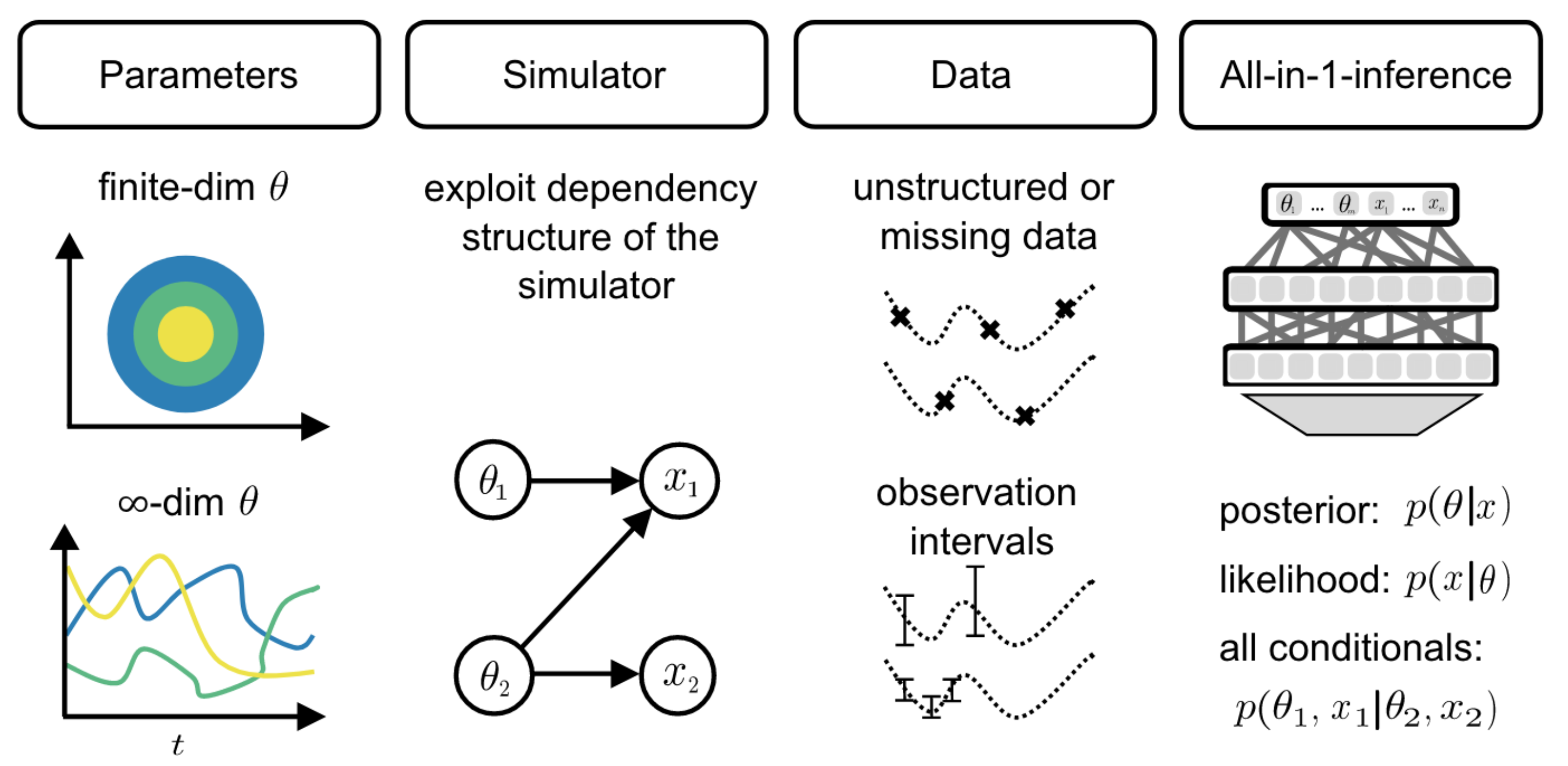
Figure 1 [Glo24A]: All-in-one simulation-based inference. Given a prior over parameters, a simulator and observed data, the Simformer can infer the posterior, likelihood and other conditionals of parameters and data.
Once trained, this so-called Simformer has the following properties (Figure 1):
- It handles both parametric and non-parametric (i.e., $\infty$-dimensional) simulators,
- can take into account known dependencies from the simulator
- takes into account known dependencies from the simulator
- allows sampling all conditionals from the joint distribution,
- and can be conditioned on intervals, i.e., ranges of data or parameter values.
These remarkable properties emerge from the design of the Simformer: a transformer architecture with SBI-tailored tokenizer and attention masks and the use of score-matching and guided diffusion.
A tokenizer for SBI
Transformers process inputs in the form of uniformly sized vectors called tokens. [Glo24A] propose to construct each token to consist of a unique identifier, its value and a condition state (Figure 2, top left). The condition state is a mask $M_C \in \{0, 1\}^d$ that indicates whether the given input $(\theta, x) \in \mathbb{R}^d$ is currently observed (conditioned) or unobserved (latent). During training, the mask is resampled for every iteration so that the transformer learns the representations for both condition states. For example, setting $M_C^{(i)}=1$ for data and $M_C^{(i)}=0$ for parameters corresponds to training a conditional diffusion model of the posterior distribution (and vice versa for the likelihood). To handle different data and parameter modalities, the Simformer can rely on specialized embedding networks as commonly used in SBI algorithms. Given input embeddings defined by the tokenizer, the Simformer proceeds with the common transformer architecture composed of attention heads, normalization, and feed-forward layers (Figure 2, right). The output is an estimate of the score function to be used in the common score-based training scheme (see below).
Modeling dependency structures with attention masks
Simulators are not always black boxes. For some simulators, practitioners may know about certain dependencies structures between parameters and data. For example, a subset of parameters may be independent, and others may influence only specific data dimensions. The Simformer allows to incorporate these dependency structures into the transformer architecture using attention masks $M_E$ [Wei23G] (Figure 2, lower left). The attention masks can be dynamically adapted at training and inference time, depending on the input values and condition state.
Training and inference
The Simforer is trained as a score-based diffusion model using denoising score-matching, which is explained nicely in [Glo24A] sections 2.3 and 3.3. In essence, the transformer outputs an estimate of the score for a given attention and conditioning mask, $s_{\phi}^{M_E}(\hat{x}_t^{M_C}, t)$. The transformer parameters $\phi$ are optimized using the loss
$$ \mathcal{l}(\phi, M_C, t, \hat{x}_0, \hat{x}_t) = (1 - M_C) \cdot \left( s_{\phi}^{M_E}(\hat{x}_t^{M_C}, t) - \nabla_{\hat{x}_t} \log p_t(\hat{x}_t \mid \hat{x}_0)\right), $$
where $\hat{x}_0$ is a data sample, $\hat{x}_t$ is a noisy sample, $p_t(\hat{x}_t \mid \hat{x}_0)$ is defined through the tractable noise process, and $(1-M_C)$ ensures that the loss is applied w.r.t. to the unobserved variables.
After training, the Simformer allows sampling from arbitrary conditionals, e.g., the posterior $p(\theta \mid x)$ or the likelihood $p(x \mid \theta)$ by masking the input accordingly. Samples are generated by integrating the reverse diffusion process on all unobserved variables and holding the observed variables constant.
Observation intervals via guided diffusion
The Simformer makes it possible to condition not only on fixed observed values but on observation intervals, e.g., to obtain posterior distribution given on a range of possible data values. This is achieved via guided diffusion with arbitrary functions [Ban23U], a technique to sample from a diffusion model given additional context $y$. See paper section 3.4 and appendix A2.2 for details.
Results
[Glo24A] evaluate their Simformer approach on four common and two new SBI benchmarking tasks against the popular SBI algorithm neural posterior estimation (NPE). Additionally, they demonstrate the capabilities of their approach on two time-series models (Lotka-Volterra and SIRD) and on a popular simulator from neuroscience (Hodgkin-Huxley model).
Benchmarking
On the benchmarking tasks, the Simformer outperforms NPE in terms of posterior accuracy, as measured in classification two-sample test accuracy (C2ST, Figure 3, left column). Notably, by exploiting known dependencies in the benchmarking tasks, the Simformer can be substantially more simulation efficient than NPE (Figure 3, orange and dark red lines). Additionally, the Simformer performed well in terms of C2ST when challenged to estimate arbitrary posterior conditionals (Figure 3, right column).
Time-series data
For the application to the Lotka-Volterra model, the Simformer was trained on the full time series data and then queried to perform inference given only a small set of unstructured observations (Figure 4). Because of its ability to generate samples given arbitrary conditionals, it is now possible to condition the Simformer only on the four observations and to obtain posterior samples (Figure 4, panel a right) and posterior predictive samples (Figure 4, panel a left) simultaneously and without running the simulator. When given more observations, the posterior and posterior predictive uncertainties decrease, as expected (Figure 4, pabel b).
The authors further use the SIRD-model to demonstrate how to perform inference with infinite-dimensional parameters (section 4.3), and the Hodgkin-Huxley model to show the use of guided diffusion to perform inference given observation intervals (section 4.4).
Limitations
Despite its remarkable properties of arbitrary conditioning, simulation efficiency and exploitation of dependency structures, the Simformer also comes with limitations. Compared to normalizing flow-based architectures (like NPE), it inherits the limitations of diffusion models that sampling and evaluation require solving the reverse SDE. Additionally, it requires substantially more memory and computational resources during training compared to normalizing flows.
An implementation of the Simformer and code to reproduce the paper results is available on GitHub. It has not been incorporated into one of the common SBI software packages yet.