Operator learning is an attractive alternative to traditional numerical methods, pursuing to learn mappings between (continuous) function spaces (like the solution operator of a PDE) with deep neural networks. In practice, though, continuous measurements of the input/output functions are infeasible, and the observed data are provided as point-wise finite discretization of the functions.

Deep operator networks (DeepONets) [Lu21L] and neural operators (such as FNO) [Kov23N] are two key architectures in operator learning. DeepONets evaluate the input function using fixed collocation points, while neural operators use uniform grid-like discretizations. As a result, neither architecture can be applied to mesh-independent operator learning, where the discretization format of the input or output function is not predetermined.

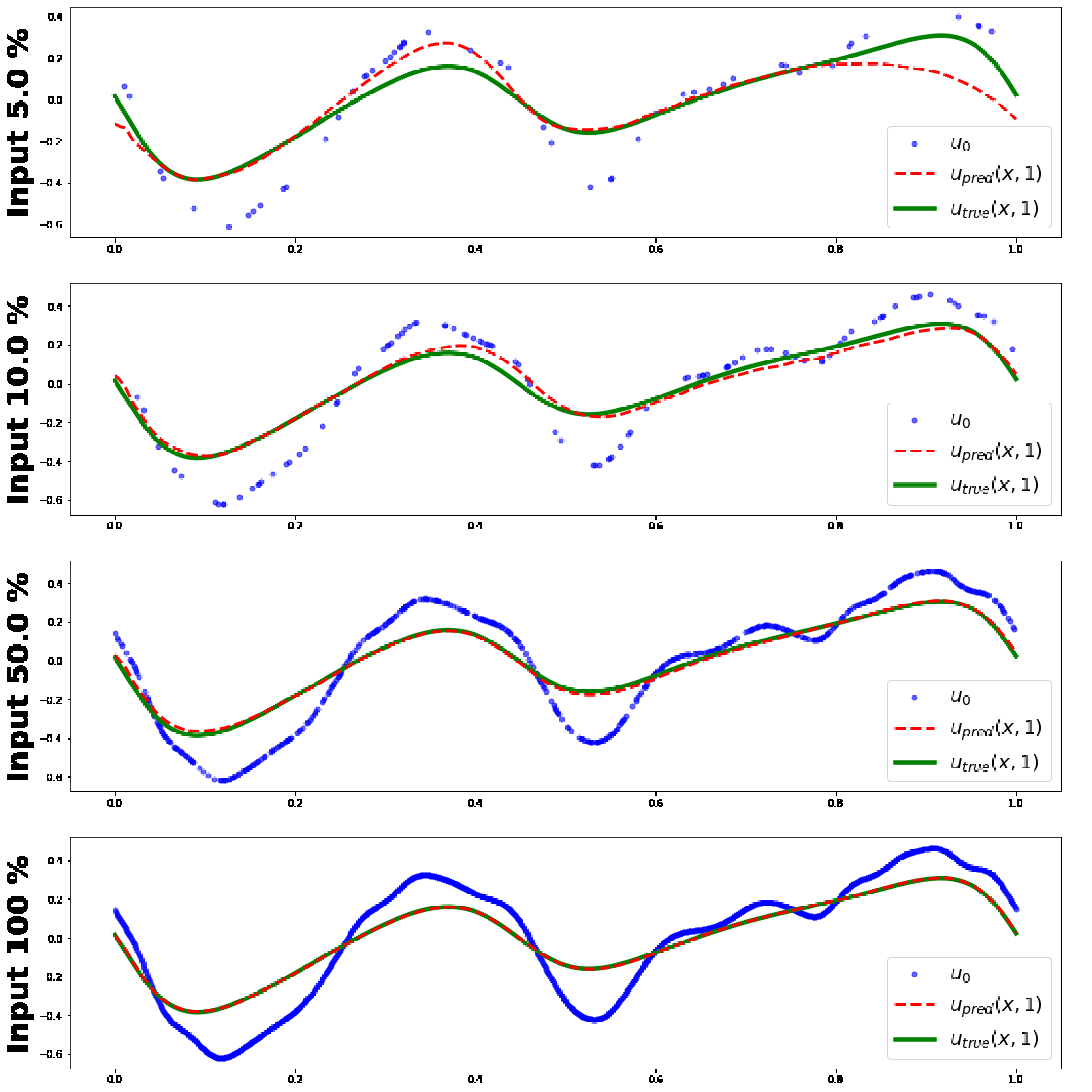Figure 2 [Lee22aM] Ground truth solutions (green lines) and predictions of MINO at query locations (red dashed lines) given the varying size of discretized inputs (blue points) for Burgers’ equation.

In real-world applications, measurements of a system are often sparsely and irregularly distributed due to the geometries of the domain, environmental conditions, or unstructured meshes. This is why the following two additional requirements should be considered for a neural operator, which are referred to as mesh-independent operator learning:

1. The output of a neural operator should not depend on the discretization of the input function.
2. The neural operator should be able to output the mapped function at arbitrary query coordinates.

Attention as a Parametric Kernel

The paper [Lee22aM] proposes the mesh-independent neural operator (MINO), a fully attentional architecture inspired by variants of the Transformer architecture [Vas17A].

The construction is inspired by the neural operator framework [Kov23N] of consecutive integral kernel integrations. Such an integration is a mapping of a function $u(x)$ defined for $x \in \Omega_x$ to the function $v(y)$ defined for $y \in \Omega_y$, using a kernel integral operation

\begin{equation} v(y) = \int_{\Omega_x} \mathcal{K}(x, y) u(x)~dx, \end{equation}

where the parameterized kernel $\mathcal{K}$ is defined on $\Omega_x \times \Omega_y$.

For input vectors $X \in \mathbb{R}^{n_x \times d_x}$ and query vectors $Y \in \mathbb{R}^{n_y \times d_y}$, treated as an unordered set, the attention layers in the MINO take the following form:

$$ \begin{aligned} Att(Y, X, X) &= \sigma(Q K^T) V \\ &\approx \int_{\Omega_x} \left(q(y) \cdot k(x)\right) v(x)~dx \end{aligned} $$

where $\quad Q = YW^q \in \mathbb{R}^{n_y \times d_q},\quad$ $K = XW^k \in \mathbb{R}^{n_x \times d_q},\quad$ $V = XW^v \in \mathbb{R}^{n_x \times d_v},\quad$ and $\sigma$ are the query, key, value matrices, and softmax function, respectively. The attention transform $Att(Y, X, X)$ can thus be interpreted as a parametric kernel $\mathcal{K}(x, y)$.

The interesting thing is that the output of the attention mechanism $Att(Y, X, X)$ is permutation-invariant to $X$ and permutation-equivariant to $Y$, i.e., for an arbitrary permutations $\pi$ and $\rho$ of $X$ and $Y$, respectively, we have

$$ Att(Y, \pi X, \pi X) = Att(Y, X, X), $$ $$ Att(\rho Y, X, X) = \rho Att(Y, X, X). $$

The MINO architecture is a stack of such attention layers and, therefore, preserves these properties!

Mesh-Independent Neural Operator (MINO)

The values of the input function $u$ are concatenated with position coordinates, $a \in \mathbb{R}^{n_x \times (d_x + d_u)}$ $$ a := \{(x_1, u(x_1)), …, (x_{n_x}, u(x_{n_x}))\}, $$ and put into the first (encoder) layer, reducing the number of inputs to a number $n_z$ of trainable queries $Z_0 \in \mathbb{R}^{n_z \times d_z}$, $$ Z_1 = Att(Z_0, a, a). $$ Afterwards, a sequence of subsequent self-attention (processor) layers $Z_l$ is applied, $$ Z_{l+1} = Att(Z_l, Z_l, Z_l), \quad l = 1, …, L-1, $$ and the final (decoder) cross-attention layer is $$ v(Y) = G_\Theta(u)(Y) = Att(Y, Z_L, Z_L), $$ evaluating the solution function at the query coordinates $Y$.

Because the first operation is permutation-invariant to the elements of $a$ (and independent of the size of the input $n_x$), the processor layers preserve the permutation-equivariant property of the attention mechanism, and the decoder layer can be queried at arbitrary coordinates $Y$, the MINO architecture is mesh-independent!

Experiments

The paper includes a set of comprehensive experiments for PDEs to evaluate MINO against other existing representative models. The results indicate that it is not only competitive, but also robustly applicable in extended tasks where the observations are irregular and have discrepancies between training and testing measurement formats, cf. Figure 2 and Table 1.

Conclusion

The MINO architecture is a promising step towards mesh-independent operator learning, allowing to represent the discretized system as a set-valued data without a prior structure, and we’re excited to see how this architecture, the first one leveraging the attention mechanism, performs in our benchmarks within continuiti!

Further Reading and Seminar

A follow-up work [Lee23I] extends the MINO architecture to the inducing neural operator (INO), which is more computationally efficient and can be applied to larger-scale problems. For more on this topic, you can refer to our seminar featuring Seungjun Lee, the author of the paper, who gave a talk on INO.