In [Kov23N], the authors introduce neural operators as a general deep-learning framework designed to learn mappings between infinite-dimensional function spaces. Traditional neural networks fall short in this application due to their dependence on the discretization of training data. Neural operators as discretization-invariant models can accept any set of points in the input and output domains and can refine towards a continuum operator. This feature makes them particularly useful in solving differential equations where input and output are function spaces.

Consider an operator $G^{\dagger}: \mathcal{A} \to \mathcal{U}$ that maps from a function space $\mathcal{A}$ to another function space $\mathcal{U}$. We aim to build an approximation of $G^{\dagger}$ by constructing a parametric map

$$ G_\Theta: \mathcal{A} \to \mathcal{U}, \qquad \Theta \in \mathbb{R}^p, $$ that minimizes the empirical risk

$$ \min_{\Theta \in \mathbb{R}^p} \mathbb{E}_{a \sim \mu} \Vert G^{\dagger}(a) - G _\Theta(a) \Vert^2 _\mathcal{U} $$

where $a \sim \mu$ are i.i.d. samples drawn from some probability measure $\mu$ supported on $\mathcal{A}$. Since $a$ are, in general, functions, to work with them numerically, one assumes access only to their point-wise evaluations.

The outlined neural operator framework has the following overall structure: A point-wise lifting operator $P$ maps the input function to its first hidden representation. Then, $T$ layers of iterative kernel integration map each hidden representation to the next integrating local linear operators and pointwise non-linearity operations. Finally, a projection operator $Q$ maps the last hidden representation to the output function, cf. Figure 2.

Figure 2 [Kov23N]: The input function $a$ is passed to a pointwise lifting operator $P$ that is followed by $T$ layers of integral operators and pointwise non-linearity operations $\sigma$. In the end, the pointwise projection operator $Q$ outputs the function $u$. Three instantiation of neural operator layers, GNO, LNO, and FNO are provided.

The framework mimics the structure of a traditional finite-dimensional neural network and can be written as $$ G_\Theta := Q \circ \sigma_T(W_{T-1} + K_{T-1} + b_{T-1}) \circ \dots \circ \sigma_1(W_0 + K_0 + b_0) \circ P, \label{eq:neural_operator} $$ where $W_t$ and $K_t$ are the local linear and integral kernel operators, respectively. The basic form of the integral kernel operators $K_t$ is essentially given by

$$ (K_t(v_t))(x) = \int_{D_t} \kappa^{(t)}(x, y) v_t(y) dy \quad \forall x \in D_{t+1}, $$

where $\kappa^{(t)}$ is a continuous kernel function. The paper discusses different ways of parameterizing the infinite dimensional architecture, in particular, the kernel function $\kappa^{(t)}$, as computing the integral is intractable. The proposed parameterizations are Graph Neural Operators (GNO), combining Nyström approximation with domain truncation, Low-rank Neural Operators (LNO), directly imposing that the kernel is in a tensor product form, and Fourier Neural Operators (FNO), considering the kernel representation discretized in Fourier space.

Remarkably, the paper draws a parallel between the DeepONet architecture and the neural operator framework, and states that a neural operator with a point-wise parameterized first kernel and discretized integral operators yields a DeepONet. Furthermore, it is shown that the proposed neural operator framework can be viewed as a continuum generalization of the popular transformer architecture.

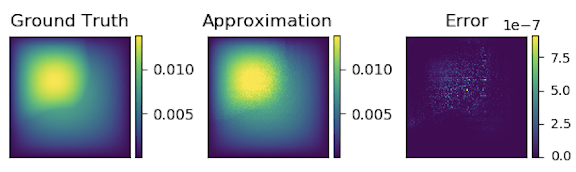Figure 9 [Kov23N]: Darcy, trained on 16 × 16, tested on 241 × 241 Graph kernel network for the solution of (6.2). It can be trained on a small resolution and will generalize to a large one. The Error is point-wise absolute squared error.

The paper studies the performance of neural operators in detail on several test problems, e.g., solving standard PDEs such as Poisson, Darcy, and Navier-Stokes equations, where it empirically demonstrates superior performance compared to existing methodologies. Specifically, the FNO architecture obtains the lowest relative error for smooth output functions, but it struggles with the advection problem since it has discontinuities. It is noteworthy that the neural operator framework can also straightforwardly be applied to super-resolution problems, cf. Figure 9.

In summary, the proposed neural operator points in an exciting direction as it is a blackbox surrogate model for function-to-function mappings. It naturally fits into solving PDEs for physics and engineering problems where it outperforms classical numerical methods in terms of speed by orders of magnitude, and it is easily applied on other problems, e.g., computer vision when images are seen as real-valued functions on 2D domains. On the downside, some methods are computationally expensive or only applicable to smooth functions on simple domains, so there is still plenty of room for improvement.

If you are interested in using neural operators in your applications, check out continuiti, our Python package for learning function operators with neural networks.