Normalizing flows are versatile density estimators and currently one of the top-performing model types for this task. However, it has been observed that normalizing flows often struggle to accurately estimate the density in areas where the support of the data distribution is thin. The paper [Kim20S] attributes this phenomenon to the inability of normalizing flows to accurately model distributions with lower-dimensional support. The authors propose a simple yet effective method for training continuous and discrete normalizing flows on distributions and point clouds where the support manifold has a lower dimension than the input space.

Normalizing Flows on lower-dimensional manifolds

Normalizing flows are designed to be diffeomorphisms in $\mathbb{R}^d$ where $d$ is the dimension of the input space. However, many real-world distributions are supported on lower-dimensional manifolds. For example, in simple data such as MNIST, the lower dimensionality of the support can easily be seen by the fact that the corners of the image are always black. In more complex data, the support manifold is not as obvious, but lower-dimensional structures are still very likely to exist.

Figure 1: Illustration of a normalizing flow trained on 2D data (top) and a 1D manifold (bottom). Yet, normalizing flows are trained as if the support manifold was the full input space. As a consequence, a distribution of full support is trained to approximate a distribution with lower-dimensional support. As such an approximation becomes tighter, the Jacobian determinant must necessarily explode, which leads to numerical instabilities. Indeed, a manifold of lower dimension has Lebesgue measure $0$ and therefore the approximated densities at the true support manifold approach infinity, which has been further investigated in subsequent work, e.g. [Mcd22C]. As a consequence, the change of variables formula becomes invalid in the limit. The paper argues that many shortcomings of normalizing flows, as seen e.g. on various 2D benchmark datasets, can be attributed to this issue. While there has been previous work on normalizing flows on lower-dimensional manifolds, the authors argue that these methods either are not numerically stable or need prior knowledge such as the dimension of the manifold.

SoftFlow

In this paper, the authors propose a simple yet effective method to train normalizing flows on distributions and point clouds where the support manifold has a lower dimension than the input space. The key idea is to train an amortized conditional flow on the data distribution perturbed with Gaussian noise conditioned on the noise level. More formally, the flow is trained to approximate the following distribution: $ p(Y | \sigma) = p(X + Z)$, where $Z \sim \mathcal{N}(0, \sigma^2I)$ and $X$ is distributed according to the data distribution $p_D$. Note that by perturbing the data with Gaussian noise, the support of the distribution is extended to the full input space. Since the flow is conditioned on the noise level $\sigma$ and trained on noise levels between $0$ and a given $\sigma_{\text{max}} > 0$, the flow learns to recover a tight approximation of the original distribution by setting $\sigma=0$ during inference.

SoftPointFlow

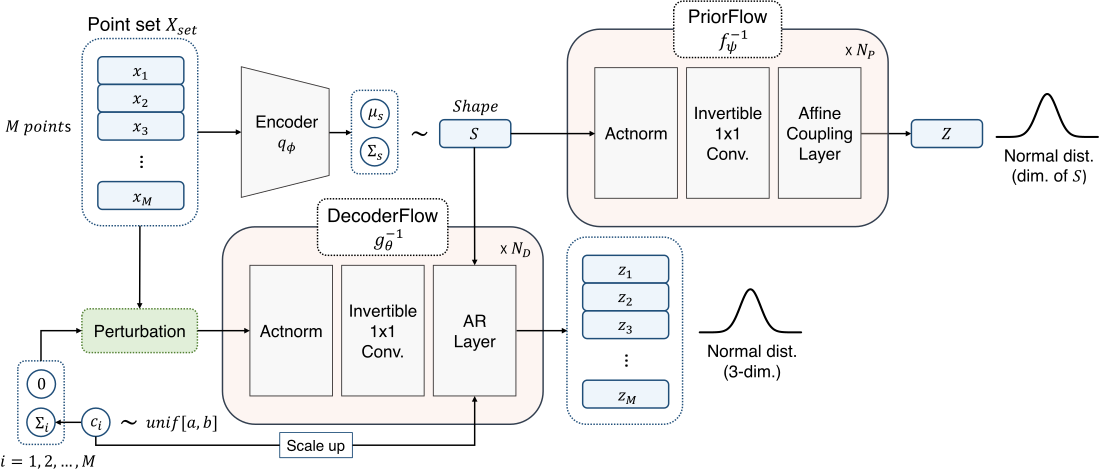Figure 3: The SoftPointFlow architecture. 3D point clouds are compact representations of the geometric details of objects. Their increasing popularity is also motivated by the fact that they can be easily acquired by range scanning devices such as LiDARs. PointFlow is a popular architecture for point cloud generation. Apparent problems with modeling thin structures, however, lead the authors of [Kim20S] to conjecture that the support of the point cloud distribution is lower-dimensional than the input space. The authors propose SoftPointFlow, a simple modification of PointFlow that uses the SoftFlow architecture to model the support manifold. SoftPointFlow is a variational auto-encoder-like architecture, where an encoder computes the posterior of the latent shape variable $S$ given the point cloud $X$, $p_\phi(S | X)$, and a decoder, implemented as SoftFlow computes the likelihood of the point cloud given the latent shape variable, $p_\theta(X | S)$. Additionally, the prior of $S$ is modeled by a PriorFlow, $p_\psi(S)$. The model is trained by maximizing the following ELBO objective: \begin{align*} &L(X_{\text{set}}; \theta, \psi, \phi) = \\ &\mathbb{E}_{q_{\phi}(S|X_{\text{set}})}\left[\log \frac{p_{\theta}(X_{\text{set}}|S, \sigma)p_{\psi}(S)}{ q_{\phi}(S|X_{\text{set}})}\right] \end{align*}

Experimental results

Figure 4: Samples from SoftFlow, Glow, and FFJORD trained on 5 different distributions. The experiments validated the proposed framework where SoftFlow was implemented within the FFJORD architecture, augmented with a noise distribution parameter. SoftFlow and FFJORD, and a 100-layer Glow model, were trained on data from five different distributions. The results indicate that Glow performed poorly across most distributions, and FFJORD also struggled, particularly with circular distributions. In contrast, SoftFlow effectively generated high-quality samples that closely followed the data distribution. Additional tests varying the noise distribution parameter demonstrated SoftFlow’s ability to accurately reflect different distributions, suggesting its potential for estimating unseen distributions or creating synthetic ones.

Figure 6: Generation results on $1$-NNA (%). Lower is better

Discussion

Because of the simplicity of the procedure, it is relatively easy to adopt SoftFlow training within existing pipelines. We have implemented the procedure in our VeriFlow project in the context of neuro-symbolic verification and can confirm that the method provides a significant improvement in the quality of the generated samples.