Deep generative models often fail to accurately capture extreme events that are observable in the real world. Major challenges for modelling multivariate extremes are heavy tailed marginal distributions and asymmetric tail dependence. Normalizing flows currently set the gold standard among deep generative models with respect to tractability as they allow exact sampling and exact computation of log-likelihoods, depending on how they are trained. However, their architecture has clear weaknesses when considering the challenges that are imposed by multivariate extremes:
- Mapping a heavy tailed distribution to a light tailed such as a Gaussian cannot be Lipschitz-bounded, which makes the learning numerically unstable [Jai20T].
- Asymmetric tail dependence induces locally a low-dimensional manifold structure which is a problem for normalising flows as continuous invertible maps maintain the dimensionality of manifolds [Kim20S].
In [Mcd22C] (IJCAI 2022) the authors propose to combine extreme value theory and copula theory with normalizing flows to overcome the shortcomings (if you are interested in modeling extreme events you might also want to have a look at our anomaly detection workshop ). The proposed architecture consists of two components:
- A hybrid kernel density model with parametric tail (generalized Pareto distribution) to model the one-dimensional marginal densities.
- A normalizing flow to model the copula density function.
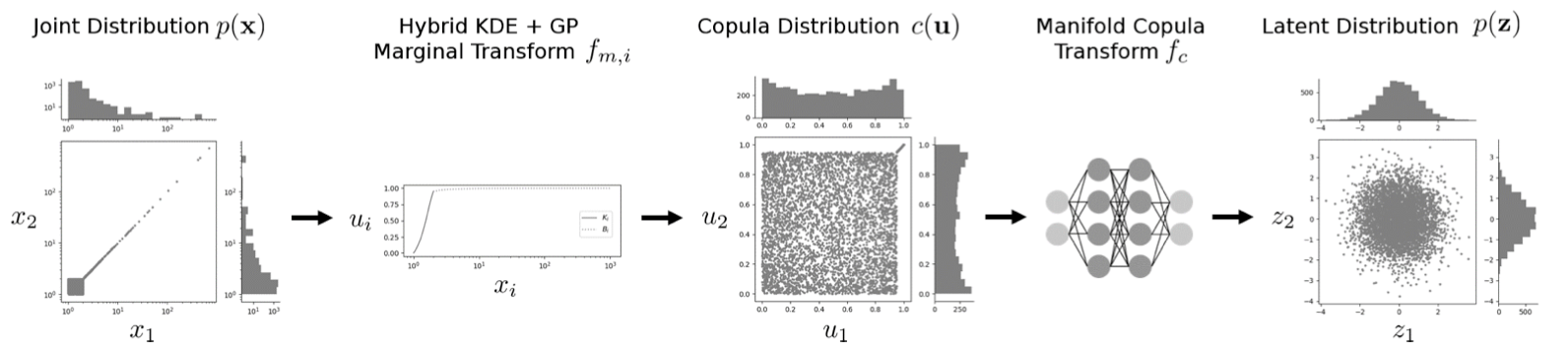
The first component tackles the challenge of heavy tails and decouples it from the dependence structure. This circumvents the need to model heavy tailed distributions by a normalising flow. However, the local low-dimensional manifold structure needs to be addressed. The authors do so by implementing ideas from the SoftFlow architecture [Kim20S] for low dimensional manifold learning: They fit a conditional flow on perturbed data where the noise level is the conditioning variable. Perturbing the data with Gaussian noise will destroy the low-dimensional structure of the original data and allow to model the perturbed distribution more precisely. By using varying noise levels at training time, the system learns to adjust the noise through the conditioning variable. Setting the noise level to zero will allow to retain the original structure at inference time.
The authors verify their idea in experiments on several benchmark data sets. The most interesting one is probably CLIMDEX, which contains climate data that is known to exhibit heavy tails and asymmetric tail dependence. They compare against several other normalizing flow architectures from vanilla RealNVPs to other architectures tailored towards improved tail modeling. COMET Flow outperforms the other architectures on heavy tailed data and does not show inferior performance on light tailed data.
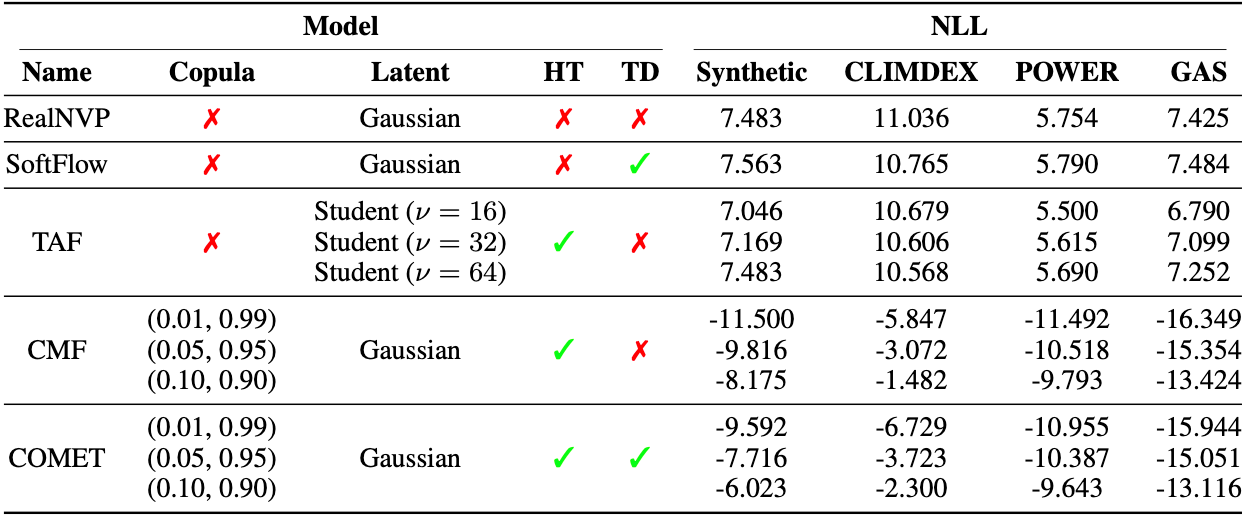
Negative log-likelihoods of various flow models on the test data sets. HT and TD indicate whether the architecture incorporates techniques to model heavy tails and tail dependence, respectively.