Deep neural operators as accurate surrogates for shape optimization

Deep neural operators, such as DeepONet, have changed the paradigm in high-dimensional nonlinear regression, promising significant generalization and speed-up in computational engineering applications. In a recent paper, the authors investigate the use of DeepONet to infer flow fields around unseen airfoils with the aim of shape constrained optimization, an important design problem in aerodynamics that typically taxes computational resources heavily.

Unlike physics-informed neural networks (PINNs) [Rai19P], a DeepONet [Lu21L] does not require any optimization during inference, hence it can be used in real-time forecasting. Traditional numerical models, such as compressible flow solvers, are computationally intensive for accurately modeling the flow field around complex airfoils. Surrogate models can alleviate the time-consuming optimization loop where the numerical solver calculates aerodynamic forces.

In a recent publication [Shu24D] in Engineering Applications of Artificial Intelligence, the authors present a case study on the use of DeepONet for airfoil shape optimization. They demonstrate empirically that DeepONet can accurately predict flow fields around unseen airfoils, cf. Figure 7, and serve as a fast surrogate for the optimization of airfoil shapes with respect to a general objective function. Figure 7: DeepONet Predictions. The pressure, density, and velocity fields around the test set airfoil NACA 7315 predicted by the DeepONet, and the corresponding pointwise absolute errors are also provided.

Specifically, the study optimizes the constrained NACA four-digit problem to maximize the lift-to-drag ratio. The results show minimal to no degradation in prediction accuracy using DeepONet while reducing the online optimization cost by approximately 30,000 times.

How much data is needed?

The crucial question is: how much data is needed to train the surrogate model? If the model requires too much data, the computational cost of training may outweigh the benefits.

Remarkably, the authors investigate using a small dataset to train the surrogate model: 40 training and 10 testing examples. Yet, DeepONet generalizes well to unseen airfoils (see Figure 9).

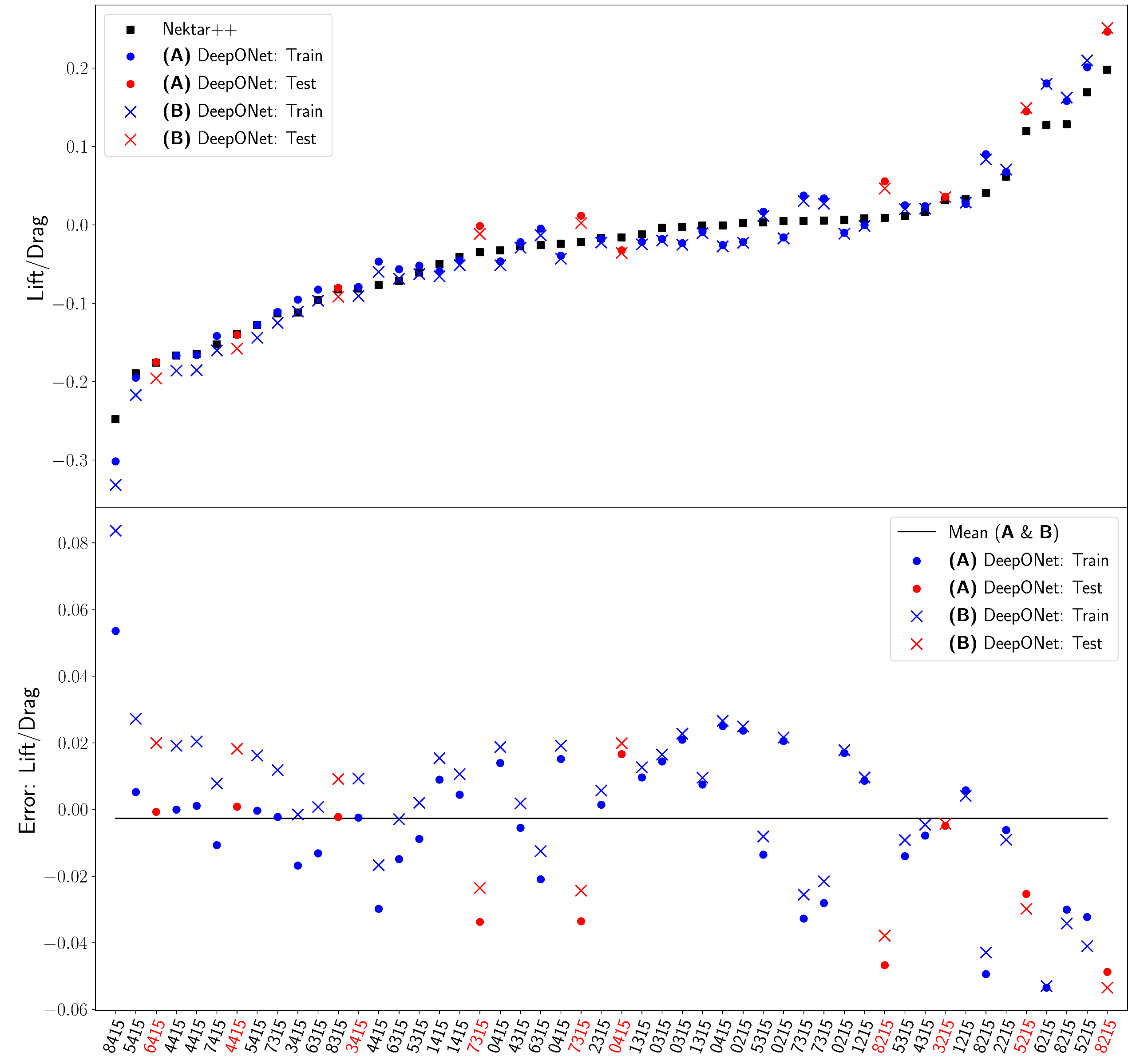
**Figure 9:** Plot of the computed lift-to-drag objective for the entire dataset sorted by the Nektar++ reference values. As seen in both plots, the approximation to the high-fidelity CFD solution is very accurate and consistent throughout the entire parametric domain. Particularly, we note that the testing set performs comparably to the training set, meaning there is little to no generalization error, which is necessary when inferring unseen queried geometries during optimization.

The paper effectively demonstrates an illustrative example within a general framework, showing how DeepONets can learn complex fluid dynamics and highlighting their potential to accelerate classical simulation tasks using deep learning.

References

[Shu24D]

Deep neural operators as accurate surrogates for shape optimization, Khemraj Shukla, Vivek Oommen, Ahmad Peyvan, Michael Penwarden, Nicholas Plewacki, Luis Bravo, Anindya Ghoshal, Robert M. Kirby, George Em Karniadakis.

Mar 2024

Deep neural operators, such as DeepONet, have changed the paradigm in high-dimensional nonlinear regression, paving the way for significant generalization and speed-up in computational engineering applications. Here, we investigate the use of DeepONet to infer flow fields around unseen airfoils with the aim of shape constrained optimization, an important design problem in aerodynamics that …

Publication

[Rai19P]

Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations, M. Raissi, P. Perdikaris, G. E. Karniadakis.

Feb 2019

We introduce physics-informed neural networks – neural networks that are trained to solve supervised learning tasks while respecting any given laws of physics described by general nonlinear partial differential equations. In this work, we present our developments in the context of solving two main classes of problems: data-driven solution and data-driven discovery of partial differential …

[Lu21L]

Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators, Lu Lu, Pengzhan Jin, Guofei Pang, Zhongqiang Zhang, George Em Karniadakis.

Mar 2021

It is widely known that neural networks (NNs) are universal approximators of continuous functions. However, a less known but powerful result is that a NN with a single hidden layer can accurately approximate any nonlinear continuous operator. This universal approximation theorem of operators is suggestive of the structure and potential of deep neural networks (DNNs) in learning continuous …

See more pills

How much data is needed?

References

In this series →