In our recent pill Beta Shapley: a Unified and Noise-reduced Data Valuation Framework for Machine Learning [Kwo22B], we discussed how relaxing the Shapley axioms and working with semi-values (i.e. allowing for certain choices of weights for the marginal utilities) makes the resulting values more useful in ML applications.
One such semi-value is the Banzhaf index, which uses a constant weight across all subsets:
$$ v_{\text{Bzf}}(x_i) = \frac{1}{2^{n-1}} \sum_{S \subseteq D \setminus \{x_i\}} [u(S \cup \{x_i\}) − u(S)] , $$
This turns out to be (very) helpful in mitigating the bane of Shapley values for supervised ML, namely: noise. For stochastic utilities, e.g. models trained with a stochastic method like SGD, there will be sets $S$ such that $u(S)$ has high variance, e.g. sets of tiny size, although in general there will be some variance for all sets.
If the coefficients weighting the marginal utility happen to be highest for those sets (as is the case for Shapley), the related values can be rather uninformative. Mitigation strategies like taking averages over multiple evaluations of $u(S)$, or generalized weights like those we saw in Beta Shapley, improve the situation but either increase the computational burden considerably or are ineffective in some contexts.
[Wan23D] addresses exactly the issue of noise in the estimate of the utility. The authors begin by introducing a definition of sensitivity to variance in the utility, in a worst-case sense: semi-values are measured according to what’s the largest noise in the utility they can tolerate before flipping the rank of samples when sorted according to their values.
Then they show that Banzhaf performs best wrt. this definition, i.e. it ensures maximal rank stability, but also the best Lipschitz constant among all semi-values, both in $\ell_2$ and $\ell_\infty$. This results in an impressive improvement in Spearman correlation wrt. vanilla Shapley across runs. The intuition for this is simple: for any given choice of weights for a semi-value, one can construct a utility with high variance where the weights are highest. In such a worst-case scenario, the best one can do is to take a constant weight.
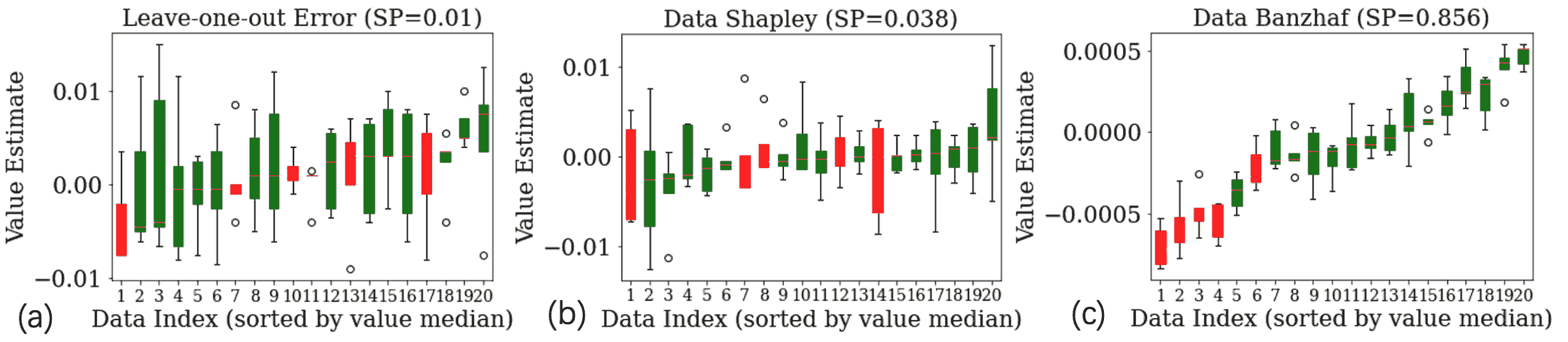
Box-plot of the estimates of (a) LOO, (b) Shapley Value, and (c) Banzhaf value of 20 randomly selected CIFAR10 images, with 5 mislabeled images. The 5 mislabeled images are shown in red and clean images are shown in green. The variance is only due to the stochasticity in utility evaluation. ‘SP’ means the average Spearman index across different runs.
The authors also tweak the standard Monte Carlo approximation to shave off a factor $n$ from the sample complexity (although this can be also achieved via caching).
If you are interested in using data valuation algorithms, as of version 0.7.0,
the TransferLab’s library pyDVL provides an
implementation of Data Banzhaf, as well as most game-theoretic methods for data
valuation, all with exact and different Monte Carlo approximations,
parallelisation and distributed caching. To try it out, install with pip install pydvl and read the documentation.