Markov decision processes (MDPs) are the prime model to capture decision-making under uncertainty. That is, MDPs and its extensions are suitable to describe how agents interact with an unpredictable and potentially hostile environment.
We take a model-centric view and ask key questions such: What is the probability to reach an error state? or What is the best policy to steer a robot to the target within a given energy budget?
In this tutorial, we present the probabilistic model checking tool Storm that can automatically answer these questions, even in the absence of precisely known models or partial observability. Storm supports various input languages such as variations of Petri nets, fault trees, and domain-specific probabilistic programming languages. It supports questions that allow trading off various objectives, provides precise results with strict guarantees, is open access, and is accessible via a Python API.
The content is based on the UAI 2022 tutorial by Professor Dr. Joost-Pieter Katoen and Dr. Sebastian Junges, two of the main researchers behind the library.
Training Resources and Materials
We understand the importance of sharing knowledge, hence, along with the recorded training from Dec. 1st 2023, we also provide the code and slides used during the training. These resources are available in the accompanying GitHub repository. This will allow you to follow along with the training at your own pace and experiment with the code to gain a deeper understanding.
We hope you find this training useful and encourage you to reach out with any questions or feedback. Also, check out our other courses on popular topics in Artificial Intelligence and Machine Learning.
Learning outcomes
By the end of this workshop, you will have gained a solid understanding of the theory behind probabilistic model checking. You will be introduced to the most important algorithms in this field. The training will guide you on how to model systems as Markov chains and Markov decision processes. You will also learn how to formulate queries about the behavior such a system. Lastly, you’ll be able to use the Storm probabilistic model checker effectively.
Structure of the workshop
Part 1: Fundamentals of Probabilistic Model Checking
We will start with an introduction into the basics of probabilistic model checking. We will discuss the important notions of Markov chains and Markov decision processes and define the semantics of the temporal logics LTL and CTL.
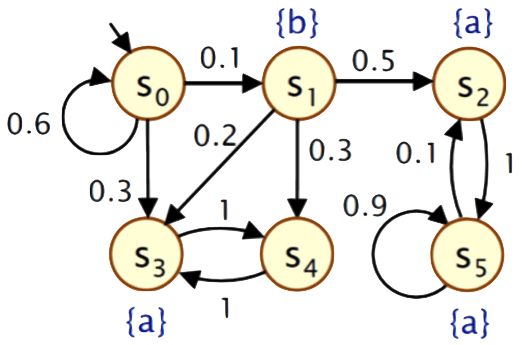
A finite state Markov chain with transition probabilities.
Part 2: Fault Tree Analysis
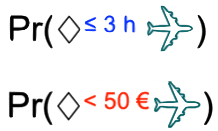 A multi-objective query in LTL
A multi-objective query in LTLFault tree analysis is a popular technique in safety and reliability engineering. Dynamic fault trees are a flexible model that is able to capture common dependability patterns, such as spare management, functional dependencies, and sequencing. We will discuss how to use Storm to analyze dynamic fault trees.
Part 3: Hands-on probabilistic Model Checking with Storm
We will then move on to a hands-on session where we will use the Storm probabilistic model checker to verify properties of some simple models.
Knuth-Yao die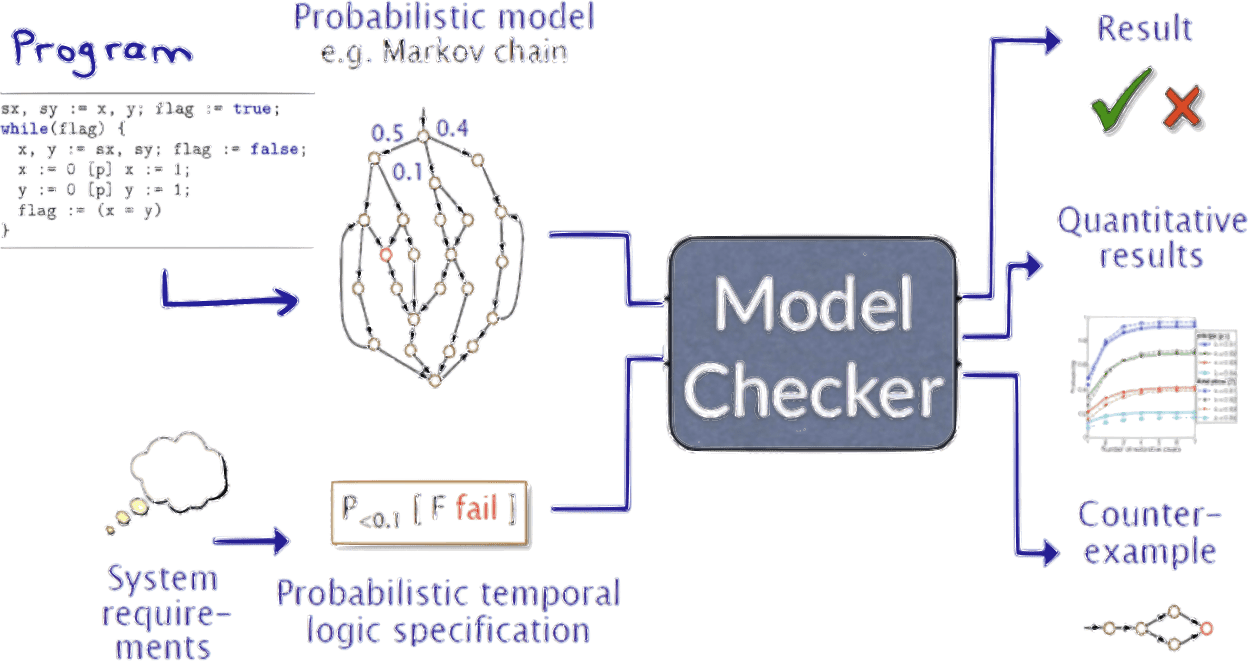 Efficient probabilistic model checking
Efficient probabilistic model checking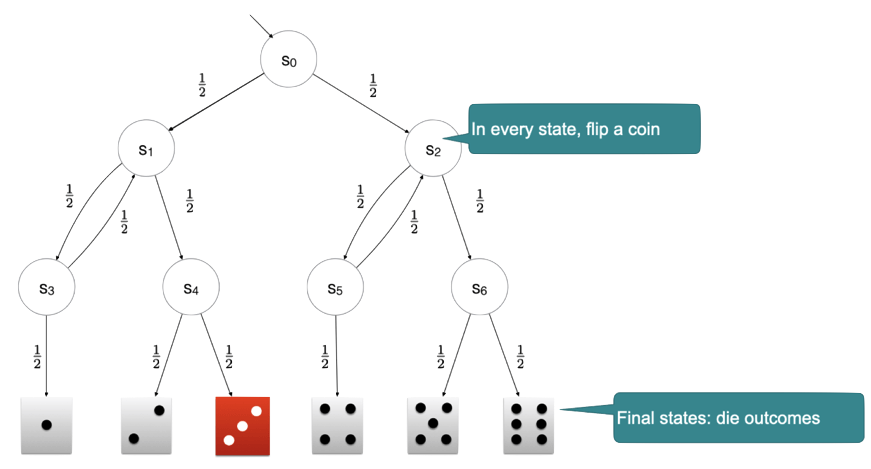
Part 4: Parameter Synthesis in Markov Models.
So far, we have only considered the case where the parameters of a Markov model are known. In many applications, however, some parameters are free to choose. In this part, we will discuss how to synthesize parameters of a Markov model such that a given specification is satisfied with high probability.
- Parameter synthesis in Markov models.
Prerequisites
- Basic knowledge of probability theory.
- Basic programming skills in Python are required.
- No prior knowledge of machine learning is required.