Prelude
Finding a set of well-performing hyperparameters often proves to be an enormously time- and resource-consuming task. Naive strategies include relying on luck, magic hands, grid search or graduate student descent. A convenient alternative is to follow the “learning instead of handcrafting” paradigm and deploy automatic hyperparameter optimisation via a higher level objective function. This paper pill covers the recent work [Eim23H], which proposes a hyperparameter optimisation and evaluation protocol for deep RL. We restate the manuscript’s depiction of the algorithm configuration (AC) problem:
Given an algorithm $A$, a hyperparameter space $\Lambda$, as well as a distribution of environments or environment instances $\mathcal{I}$, and a cost function $c$, find the optimal configuration $\lambda^* \in \Lambda$ across possible tasks s.t.: \begin{equation} \lambda^* \in \arg \min_{\lambda \in \Lambda} \mathbb{E}_{i \sim \mathcal{I}} [c(A(i;λ))]. \tag1\end{equation}
Usually, the HPO process is terminated according to some budget before the optimal configuration $\lambda^*$ is found. The solution found by the HPO process is referred to as the incumbent. Note that this expression takes the expectation over environment instances $i \sim \mathcal{I}$.
In reinforcement learning, the cost function is usually the average return obtained by the algorithm. After setting up the problem, the authors dive into the impact of different hyperparameter choices on final performance.
Which hyperparameters matter in deep RL
The paper considers basic gym environments (Pendulum or Acrobot), gridworlds with an exploration component (Minigrid) and Brax’s (our pill) robot locomotion tasks like Ant, Halfcheetah or Humanoid. The algorithms handled are Proximal Policy Optimisation (PPO) [Sch17P] (our blog) and Soft Actor Critic (SAC) [Haa18S] for continuous environments, and Deep Q-learning (DQN) [Mni13P] and PPO for discrete environments. All implementations are taken from StableBaselines3.
The hyperparameters considered for PPO are 11 quantities like learning rate, entropy coefficient, clip range and so on. Figure 1 shows a selected subset of results. For different combinations of algorithm and environment, one hyperparameter is varied, and the returns obtained across 5 seeds (different from the training seeds) are plotted.
Figure
1. [Eim23H], Figure 2. Hyperparameter
landscapes of learning rate, clip range and entropy coefficient for PPO on Brax
and MiniGrid. For each hyperparameter, the average final return and standard
deviation across 5 seeds is reported.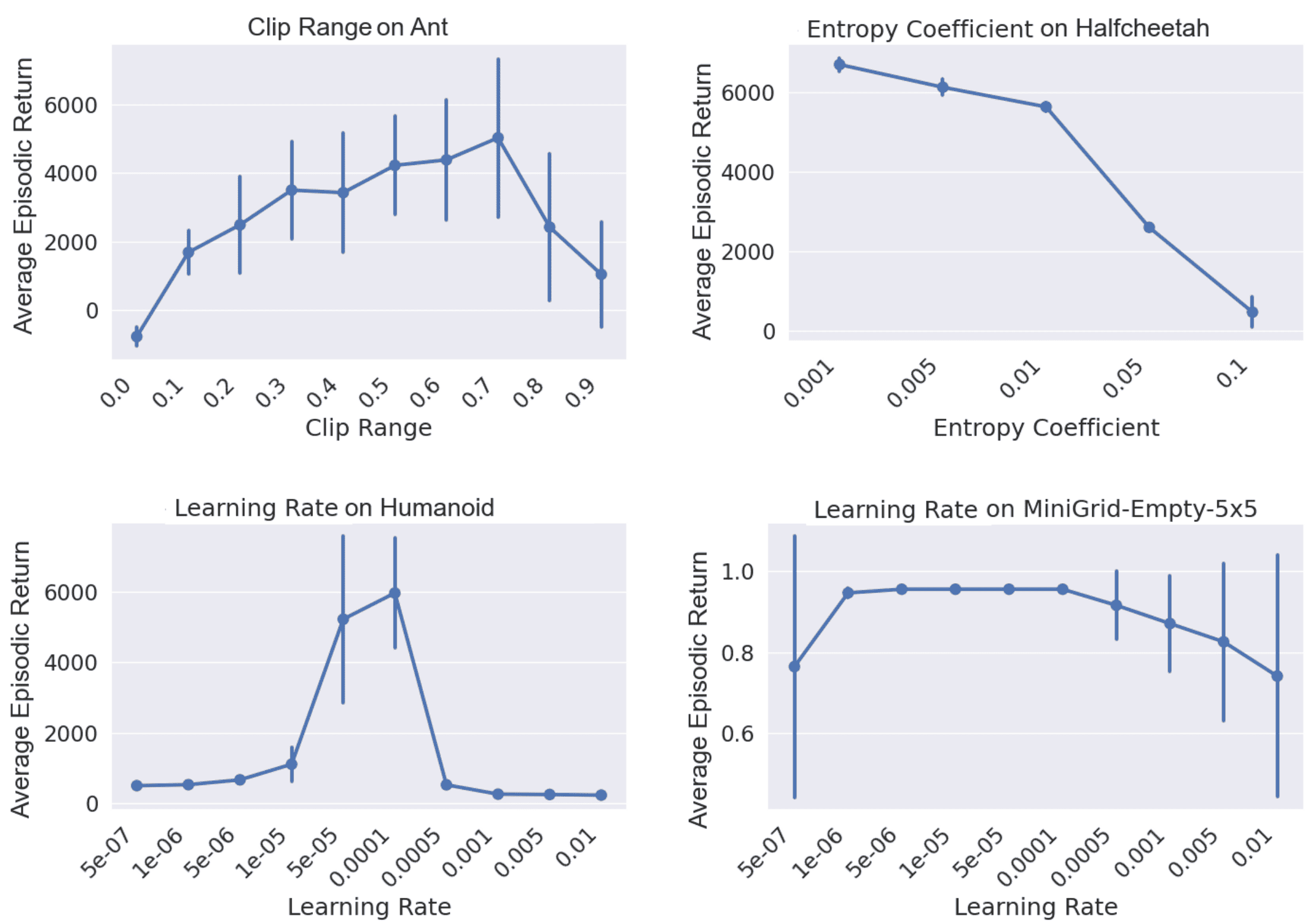
The authors conclude: "… hyperparameter importance analysis using fANOVA … one or two hyperparameters monopolize the importance on each environment … tend to vary from environment to environment (e.g. PPO learning rate on Acrobot, clip range on Pendulum and the GAE lambda on MiniGrid - see Appendix I for full results). … Partial Dependency Plots on Pendulum and Acrobot (Appendix J) show that there are almost no complex interaction patterns between the hyperparameters which would increase the difficulty when tuning all of them at the same time." While [Eim23H] focus on the impact of different numeric hyperparameters, the work by Andrychowicz et al. [And20W] covers a broader range of possible design choices (though only for on-policy algorithms on Mujoco tasks).
As there is no subset of hyperparameters that is consistently the most important across different environments, HPO has to be performed over the full search space of all hyperparameters. In such a scenario, naive grid search becomes intractable, manifesting a clear need for more advanced HPO algorithms in RL. There is, however, an added difficulty in RL compared to supervised learning, namely the dependence on the random seed.
How to do HPO in RL
While the performance of RL algorithms is notoriously brittle, let’s start with some good news. Figure 2 shows hyperparameter configurations performing largely consistently with each other, meaning good configurations learn quickly while poor ones learn slowly or even collapse. This is great news as it allows using HPO methods relying on partial training runs.
However, inconsistent performance is also possible, as demonstrated by the bottom-left picture (PPO on Ant - Clip Range). From my personal experience, there often are cases in which one configuration plateaus while another one continues to improve and eventually reaches higher returns. So if you consider using HPO methods based on partial runs, check the consistency of runs for your task!
 Figure 2.
[Eim23H], Figure 3. Hyperparameter sweeps for PPO
over learning rates, entropy coefficients, and clip ranges on various
environments. The mean and standard deviation are computed across 5
seeds.
Figure 2.
[Eim23H], Figure 3. Hyperparameter sweeps for PPO
over learning rates, entropy coefficients, and clip ranges on various
environments. The mean and standard deviation are computed across 5
seeds.Figure 2 reveals large variance in returns for some seeds, however, mainly for configurations that perform moderately well.
This means that the behavior of a configuration might differ drastically across seeds. Figure 3 depicts the returns for several seeds of the same configuration. The x-axis shows the number of episodes, and the y-axis the average episodic return. The line patterns correspond to different seeds and the colors to different hyperparameter choices for clip range or entropy coefficient respectively.
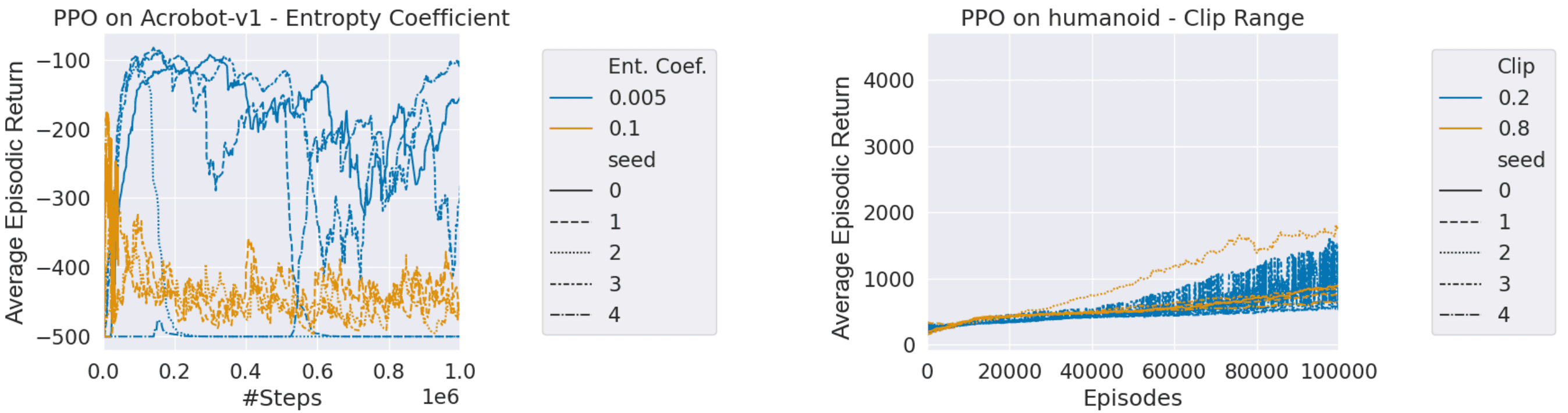
Figure 3. [Eim23H], Figure 4. Average episodic return for individual seeds (line patterns) for selected clip range and entropy coefficient values (colors) of PPO across various environments.
[Eim23H] state: " … previously predictable behaviour is replaced with significant differences across seeds. We observe single seeds with crashing performance, inconsistent learning curves and also exceptionally well performing seeds that end up outperforming the best seeds of configurations which are better on average … “.
The proposed solution for establishing reliable experimentation is fixing (and reporting) a set of training seeds across different algorithms. Unsurprisingly, not only the training performance depends on the seed, but also the evaluation performance. Thus, it is advisable to also fix (and report) a set of test seeds that is distinct from the training seeds. This raises the issue of how to perform HPO for RL in a reproducible and efficient manner.
Tackling the reproducibility issue, [Eim23H] proposes the following HPO protocol for deep RL:
- Define a (disjoint) training and test set which can include:
- Environment variations
- Random seeds for non-deterministic environments
- Random seeds for initial state distributions
- Random seeds for the agent (including network initialization)
- Training random seeds for the HPO tool
- Define a configuration space with all hyperparameters that likely contribute to training success;
- Decide which HPO method to use;
- Define the limitations of the HPO method, i.e. the budget (or use self-termination);
- Settle on a cost metric – this should be an evaluation reward across as many episodes as needed for a reliable performance estimate;
- Run this HPO method on the training set across a number of tuning seeds;
- Evaluate the resulting incumbent (best found hyperparameters) configurations on the test set across a number of separate test seeds and report the results.
Note that the evaluation protocol is also applicable if no HPO is performed. In this case, it boils down to defining different (disjoint) training and test seed sets.
Point 6 hides a critical aspect of the method. The AC problem suggests using the mean performance over training instances to determine the incumbent (which is also done in this paper). Recall, however, that since a large return variance over seeds occurs predominantly for moderately performing configurations (see Figure 2 and Figure 3), the choice of mean as aggregation method is questionable. A stabilising alternative might be to consider the Interquartile Mean (IQM) that was previously proposed for the reporting of results in RL [Aga21D] (or our pill).
Experimental Results
The experiments include several HPO methods:
Random Search (RS) [Ber12aR]: samples randomly from the configuration space. Sampled configurations are evaluated on full runs, and the configuration with the best performance is selected as incumbent.
Differential Evolution Hyperband (DEHB) [Awa21D]: combines ideas from multi-fidelity methods HyperBand and the evolutionary algorithm differential evolution. The idea is to start with a large set of configurations that are partially evaluated. Based on these results, a new smaller set of configurations is obtained and evaluated for a longer number of episodes. In this way, an increasing amount of computing power is spent on a decreasing set of promising configurations.
Bayesian Generational Population-based Training (BGT) [Wan22B] and Population-Based Training 2 (PB2) [Par21P]: are population based methods that maintain a fixed population of agents in parallel that are evaluated for $n$ steps. Afterwards, a portion of the worst performing agents is replaced by mutations of the best performing algorithms or newly sampled configurations in case the population of agents doesn’t show improvements.
Following the outlined evaluation protocol, the first choice to make is the set
of training seeds. One might think that given all the brittleness of deep RL it
might be better to make the set of training seeds as large as possible. However,
it turns out that sizes of 3 or 5 yield the best performance with low variance. Table 1: [Eim23H], Table 2. Tuning PPO on Acrobot (top) and SAC on
Pendulum (bottom) across the full search space according to performance mean on
training seeds sets of variable magnitude. Lower numbers are better, best
test performance for each method and values within its standard deviation are
highlighted. Test performances (mean and standard deviation) are aggregated
across 10 separate test seeds.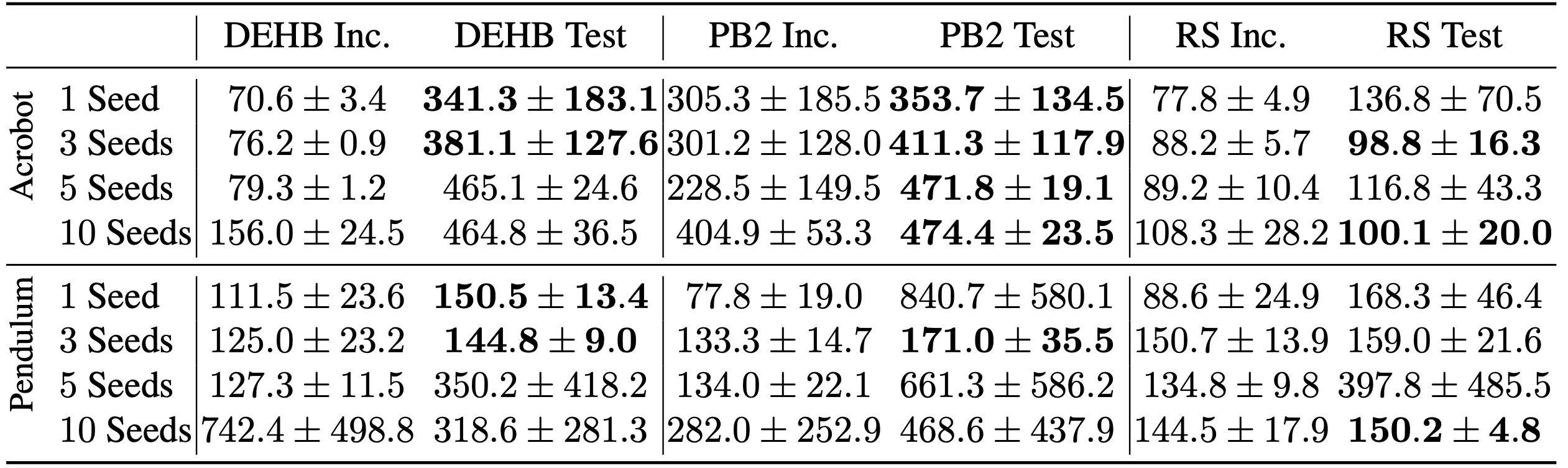
Note especially the massive variance for the training seed set of cardinality 10 on the Pendulum environment for DEHB and PB2.
The tuning process involves two budget scenarios for each tuning algorithm: a smaller one with a maximum of 16 full algorithm runs and a larger one with 64 runs. To gauge the reliability of both, the tuning algorithm and the configurations it identifies, each tuning algorithm is executed 3 times on 5 seeds and subsequently evaluated on 10 unseen test seeds. The obtained results are shown in Figure 4.
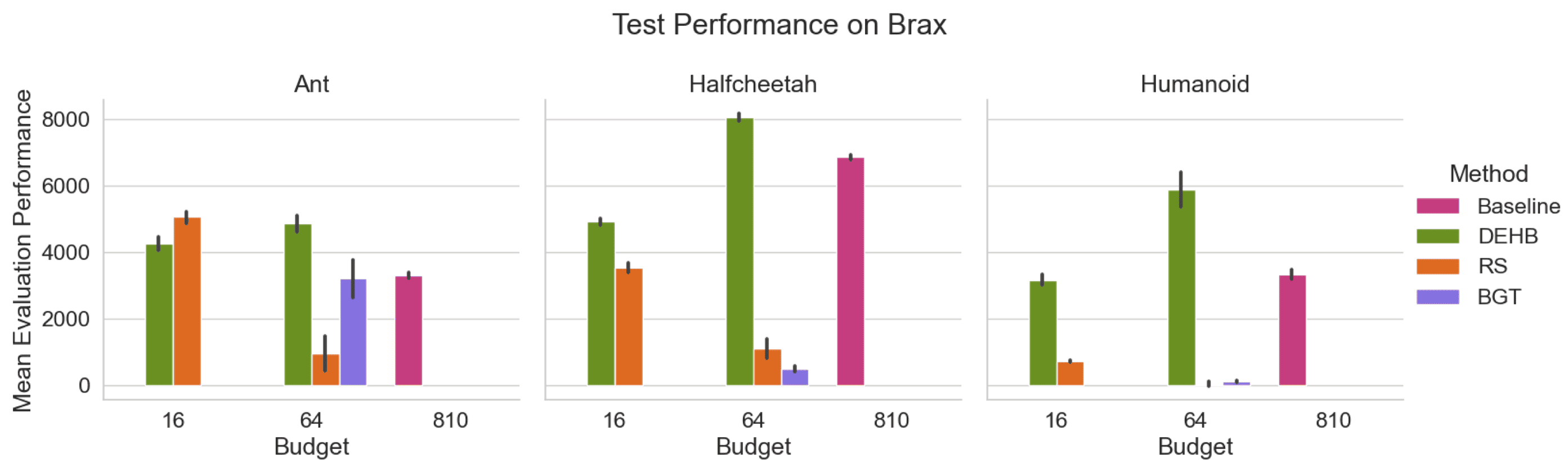
Figure 4. [Eim23H], Fig. 5. Tuning Results for PPO on Brax. Shown is the mean evaluation reward across 10 episodes for 3 tuning runs as well as the 98% confidence interval across tuning runs.
The authors conclude: ” …HPO tools conceived for the AC setting, as represented by DEHB, are the most consistent and reliable within our experimental setting. Random Search, while not a bad choice on smaller budgets, does not scale as well with the number of tuning runs. Population-based methods cannot match either; PB2, while finding very well performing incumbent configurations struggles with overfitting, while BGT would likely benefit from larger budgets than used …". For detailed results, we refer the reader to the paper.
Discussion
Bringing automated HPO into RL could pave the way for many new real world applications and accelerate scientific knowledge. The proposal of a unified (HPO) evaluation protocol is a first step in this direction. There remain a lot of open questions, such as why the HPO performance drops for larger training seed sets, which HPO methods are well suited for RL with extremely noisy/seed-dependent performance, the reliability of partial runs and others.
Especially when lacking insights into the effects of certain hyperparameters, using random search seems advantageous compared to grid search.
The code is freely available on GitHub. This work is an important step towards principled evaluation of deep RL experiments. Further work will be required to simplify the inclusion of HPO algorithms in RL projects.
Finally, I would like to invite you, dear reader, to share your thoughts about appropriate evaluation protocols and hyperparameter optimisation in deep RL.