Amortized Bayesian inference

When performing Bayesian inference given a new observation $x$, one usually obtains estimates of the posterior distribution $p(\theta | x)$ by re-running an inference algorithm, e.g., MCMC or variational inference. In contrast, amortized Bayesian inference aims to learn the mapping from observations to posterior distributions using a conditional density estimator, usually parametrized by a neural network. The potentially high initial cost of training the conditional density estimator then amortizes as we perform inference with new observations because we can obtain the posterior estimate through a single neural network forward pass.

More formally, given a fixed generative model $p(θ, x) = p(x|θ)p(θ)$, amortized Bayesian inference aims to approximate a function $f: \mathcal{X} ↦ \mathcal{P}(θ)$ that maps data to the posterior distribution $f(x_o) = p(θ| x_o)$.

Amortized simulation-based inference

The amortized Bayesian inference approach can also be applied in settings in which we do not have direct access to the generative model, e.g., in simulation-based inference (SBI), where we can only sample $(x,θ) \sim p(x|θ)p(θ)$ by drawing $θ$ from a prior and simulating data $x|θ$ from a simulator.

One method to perform amortized SBI is Neural Posterior Estimation (NPE, [Pap18F]). To perform NPE, one first draws training samples $(x,θ) \sim p(x|θ)p(θ)$ using a given prior and a simulator and then trains a conditional density estimator $q_{ϕ}(θ|x)$ to approximate the posterior distribution. $q_{\phi}$ is parametrized by, e.g., a mixture density network or a normalizing flow, and the learnable parameters $\phi$ are optimized according to

$$ \mathcal{L}(\phi) = \mathbb{E_{p(θ, x)}}[-\log q_{\phi}(θ|x)] \approx \frac{1}{N}\sum_{i=1}^{N} -\log q_{\phi}(θ_i|x_i). $$

Intuitively, by minimizing this loss, we maximize the log density of the parameters under the current estimate of the posterior. Once the conditional density estimator $q_{ϕ}(θ| x)$ is trained, posterior estimates given observed data points $x_o$ can be obtained by just a single forward pass through the neural network.

Adversarial attacks in simulation-based inference

Figure 1 [Glo23A], Adversarial attacks on amortized inference: Amortized inference via NPE passes the observed data through a neural network to obtain a posterior estimate and predictive samples that match the observed data (top, left to right, blue). An adversarial attack through a barely visible perturbation to the observed data leads to a substantially different posterior estimate and unrealistic predictive samples (middle, left to right, red). When equipped with a defense mechanism, NPE with perturbed data results in a more reliable posterior estimate and realistic predictive samples (bottom, red).

Amortized SBI with neural network-based conditional density estimators can substantially speed up Bayesian inference in scientific and engineering applications. However, this comes at a cost. First, the posterior estimates obtained from $q_{ϕ}(θ| x)$ will not be exact (only in the limit of infinite training data and an expressive enough density estimator). Second, it has been shown that neural networks can be susceptible to adversarial attacks, i.e., tiny targeted changes to the input data leading to vastly different outputs.

[Glo23A] argue that in the context of SBI, adversarial attacks can lead to substantially different posterior estimates and predictive samples, posing a potential safety risk in real-world applications of SBI (Figure 1). To mitigate this problem, they propose a regularization term in the loss function used for training the conditional density estimator, leading to more robustness against adversarial attacks. Their proposal extends previous work on adversarial robustness and introduces several techniques for making it computationally feasible in the SBI setting.

Adversarial defenses for simulation-based inference

Formally, adversarial examples for a given neural network $f$ can be obtained by solving an optimization problem [Sze14I]:

$$ \tilde{x} = \underset{||\tilde{x}-x||_{\mathcal{X}}\leq \epsilon }{\operatorname{argmax}} \Delta(f(\tilde{x}), f(x)) $$

where $\Delta$ denotes some distance measure between predictions of the neural network $f$. In other words, the attack is designed to obtain an adversarial example $\tilde{x}$ that is minimally different from $x$ but results in maximally different predictions by the neural network. In the SBI setting, an adversarial example corresponds to a minimally perturbed observed data point that yields substantially different and potentially incorrect posterior estimates.

To construct a defense for SBI against an attack with adversarial examples $\tilde{x}$, [Glo23A] build on a popular defense called TRADES [Zha19T]. TRADES aims to defend against adversarial attacks by including adversarial examples in the training data set, thereby making the neural network immune against corresponding attacks. When applied in the SBI setting, TRADES can be seen as introducing a regularization term to the original NPE loss that penalizes the difference between posterior estimates given the clean data and the adversarially perturbed data:

$$ \mathcal{L}(\phi) = \mathbb{E}_{p( \tilde{x}, x, \theta)}[-\log q_{\phi}(θ|x) +\beta D_{KL}(q_{\phi}(θ|x)|| q_{\phi}(θ|\tilde{x}))], $$ where $\beta$ is a hyperparameter scaling the strength of the regularization.

Unfortunately, this regularization scheme requires generating adversarial examples $\tilde{x}$ for each training data point $x$, which makes it computationally highly demanding and infeasible for the SBI setting.

Regularizing by the Fisher information matrix (FIM)

To adapt the TRADES defense theme to SBI, [Glo23A] propose the following. They formally define the adversarial attack to the amortized density estimator as a perturbation $\delta$ obtained by solving the constrained optimization problem

$$ \delta^* = \underset{\delta }{\operatorname{argmax}} ;
D_{KL}(q_{\phi}(θ|x)|| q_{\phi}(θ|x + \delta)) ; s.t. ; ||\delta||\leq \epsilon. $$

Note that the use of this equation can be two-fold. It yields adversarial examples for a given observation $x$, and it can be used in the TRADES defense scheme to regularize the NPE loss function.

Next, to avoid the generation of adversarial examples during training, [Glo23A] use the assumption that adversarial perturbations are small enough to approximate the KL-divergence with a second-order Taylor approximation (when expanding around $x+\delta$, the first two terms vanish; see main paper for details and references):

$$ D_{KL}(q_{\phi}(θ|x)|| q_{\phi}(θ|x + \delta)) \approx \frac{1}{2}\delta^{\top} \mathcal{I_x}\delta, $$ where $\mathcal{I_x}$ is the Fisher information matrix (FIM).

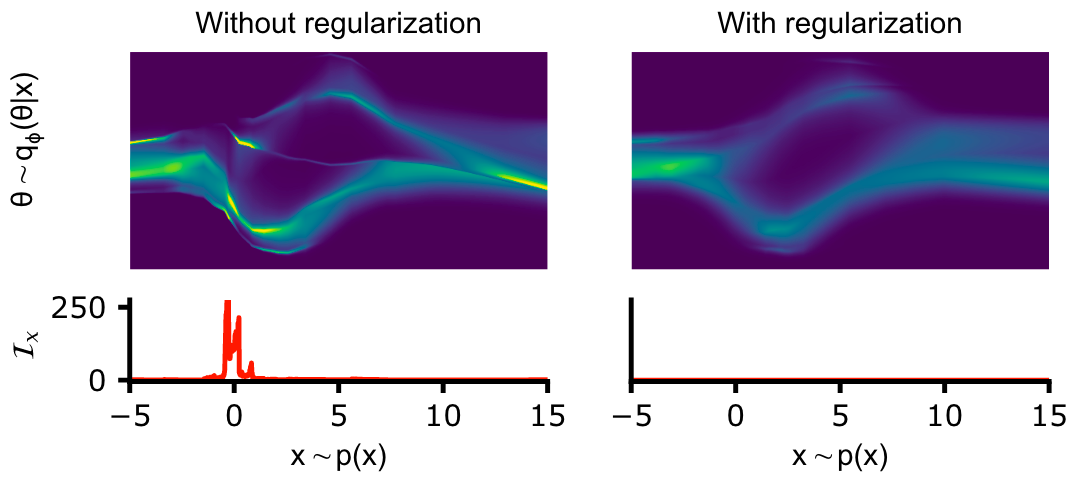Figure 2 [Glo23A], Regularizing conditional density estimators by the Fisher information matrix (FIM): The authors trained a normalizing flow with standard negative log-likelihood loss (left) and the FIM-regularized loss (right). For standard loss, the FIM reveals regions where $q_{\phi}(\theta|x)$ changes quickly as a function $x$, while the regularized loss results in smooth density estimates throughout data space.

Intuitively, the FIM characterizes how susceptible the neural network $q_{\phi}$ is to adversarial attacks in different directions in data space (see Figure 2). Specifically, the neural network is most vulnerable along the eigenvector of the FIM with the largest eigenvalue $\lambda_{max}$. Thus, to improve robustness along this direction, one can regularize the NPE loss function with that eigenvalue:

$$ \mathcal{L}(\phi) = \mathbb{E}_{p(x, \theta)}[- \log q_{\phi}(\theta | x)+ \beta \lambda_{max}]. $$

Efficient computation of the regularizer

The authors have replaced the generation of adversarial examples during training with the calculation of the eigenvalues of the FIM for every training step, which can still be costly. They propose several additional steps to reduce the computational cost of computing the regularization term during training. For expressive density estimators like normalizing flows that are commonly used in SBI, the FIM needs to be approximated with Monte Carlo sampling. To avoid a new Monte Carlo estimate at every training iteration, the authors propose a moving window average as an approximation, assuming that the neural network changes only slightly with every iteration. Additionally, instead of computing the largest FIM eigenvalue, they compute the trace of the FIM as an upper bound to the eigenvalue. Lastly, they do not save the FIM trace explicitly for every $x$ and training iteration $t$ but instead save the gradient with respect to the neural network parameters averaged over $x$ (i.e., they take the gradients separately for the original loss term and the regularizer term). Overall, this results in the FIM-regularized NPE loss

$$ \mathcal{L}_{FIM} = \mathbb{E}_{p(x, \theta)}[- \log q_{\phi}(\theta | x)]+ \beta \mathbb{E}_{p(x)}[tr(\hat{\mathcal{I}}_x^{(t)})]. $$

Empirical results

The authors use six high-dimensional benchmark tasks that they adapted from an established benchmarking framework for SBI algorithms [Lue21B]. They compare their FIM-regularized NPE loss against the standard NPE loss and two alternative defense strategies.

They use two performance metrics: The effect of the adversarial attack on the posterior estimation quantified by the KL-divergence between the posterior estimates given the clean and perturbed data, $D_{KL}(q(\theta|x)||q(\theta | \tilde{x}))$, and the expected coverage of the perturbed posterior estimates, indicating whether posterior estimates are under-, or overconfident.

Figure 5 summarizes their results and has three essential takeaways:

1. FIM-regularization performs on par with other defense methods, but it is computationally substantially more efficient and scalable, as it does not require generating adversarial examples during training (panel A).
2. The expected coverage metric shows that posterior estimates obtained with FIM-regularization all contain the underlying parameters even with strong adversarial perturbations, as desired for safe-critical applications of SBI (panel B).
3. With FIM, one can use the regularization parameter $\beta$ to trade off posterior accuracy and adversarial robustness. Panel C shows that a substantial gain in robustness only leads to a small drop in accuracy.

Lastly, the authors apply their approach to a high-dimensional and computationally demanding SBI problem from neuroscience. They find that in this challenging setting, FIM-regularization still leads to more robust and conservative posterior estimates and realistic predictive samples.