This paper pill presents the paper Seizing Serendipity: Exploiting the Value of Past Success in Off-Policy Actor-Critic [Ji23S]. During the training of an actor critic algorithm, one would expect the current policy to perform comparably to the best action in the replay buffer. The authors show that this is commonly not happening in practice. To address the performance gap between the best actions in the buffer and the current policy, they propose the Blended Exploitation and Exploration (BEE) Bellman operator. The BEE operator is a mixture of the standard Bellman operator and a novel exploitation operator designed to minimize the aforementioned performance gap.
Background
Let us consider sequential decision-making in a Markov decision process (MDP) $(S, A, P, r, H)$ with state space $S$, action space $A$, transition dynamics $P$, reward function $r$ and horizon $H$. Applying classic Q-learning to the data in the replay buffer $D = \{s_i, a_i, r_i, s’_{i}\}_{i=1}^N $ of size $N$ that were collected by all previous policies $\pi_1, \dots , \pi_k$ (or similarly the mixture of all previous policies $\mu$) amounts to training the critic parameters $\theta$ via minimizing the mean squared Bellman error:
$$ L_{TD}(\theta) = \mathbb{E}_{(s,a,r,s’) \sim D} \left[\left(r + \gamma \max_{a’ \in A} Q_{\hat {\theta}}(s’,a’) - Q_{\theta}(s,a) \right)^2\right], $$
(usually, on a minibatch of data). The term $r + \gamma \max_{a’ \in A} Q_{\hat {\theta}}(s’,a’)$ is referred to as the Bellman-target or TD-target and we denote it also as $\mathcal {T}Q_\phi(s,a)$. As the $\max_a$ is intractable for continuous or very large discrete action spaces, a policy $\pi_\phi$ is extracted from the Q-function to select the best action for any given state, for example via the training objective:
$$ L(\phi) = \mathbb{E}_{s \sim D} \left[Q_\theta(s,\pi_\phi(s)) \right]. $$
The Bellman equation used to train the critic builds the TD-target based on the current policy $\pi(s’)$ as approximation to the $\max_a$:
$$ L_{TD}(\theta) = \mathbb{E}_{(s,a,r,s’) \sim D} \left[\left(r + \gamma Q_{\hat {\theta}}(s’,\pi(s’)) - Q_{\theta}(s,a) \right)^2\right]. $$
To foster exploration, it is common to incorporate an additional exploration term $\omega(s’,a’| \pi)$ (e.g., maximum entropy or count-based exploration) into the training objective. This results in the following formulation of the Bellman-target:
$$ \mathcal{T}_{explore}Q_\theta(s,a) = r(s,a) + \left[ \mathbb{E}_{s’ \sim P(\cdot | s, a)} \mathbb{E}_{a’ \sim \pi(\cdot|s’)}[Q_\theta (s’,a’) - \omega(s’, a’| \pi) \right]. $$
The Problem addressed by BEE
In [Ji23S] Ji et al. tackle the issue that in the course of training the policy is not monotonically improving in all states. Thus, a current policy might select an action for state $s$ that is worse than the best action selected so far (which is contained in the replay buffer).
To quantify this phenomenon, the authors plot the difference between the Q-function estimate of the critic (of the current policy) and the monte carlo Q-function estimate based upon the data in the replay buffer:
$$ \Delta(\mu_k, \pi_k) = \mathbb{E}_s \left[ \max_{a \sim \mu_k(·|s)} Q(s,a) − \mathbb{E}_{a \sim \pi_k(·|s)} [Q(s,a) − \omega(s, a| \pi_k)] \right]. $$
Figure 2.
In the DKittyWalkRandomDynamics task (walking
quadruped robot), when the
agent gradually starts to solve the task in the latter stage of training
(referred to as the “under-exploitation” stage), SAC is prone to
underestimation pitfalls. The gap in $Q$ estimation is evaluated by
comparing the SAC $Q$-values and the Monte-Carlo $Q$ estimates using the
trajectories in the replay buffer.
[Ji23S] Figure 1. We expect the $Q$ value of
$(s,a)$ having been observed at least once with a successful successor $(s’,a′)$
to be high. But the Bellman evaluation operator, whose target-update actions
$a’$ are only sampled from the current policy, tends to underestimate it.
[Ji23S]
Figure 1. We expect the $Q$ value of
$(s,a)$ having been observed at least once with a successful successor $(s’,a′)$
to be high. But the Bellman evaluation operator, whose target-update actions
$a’$ are only sampled from the current policy, tends to underestimate it.
[Ji23S]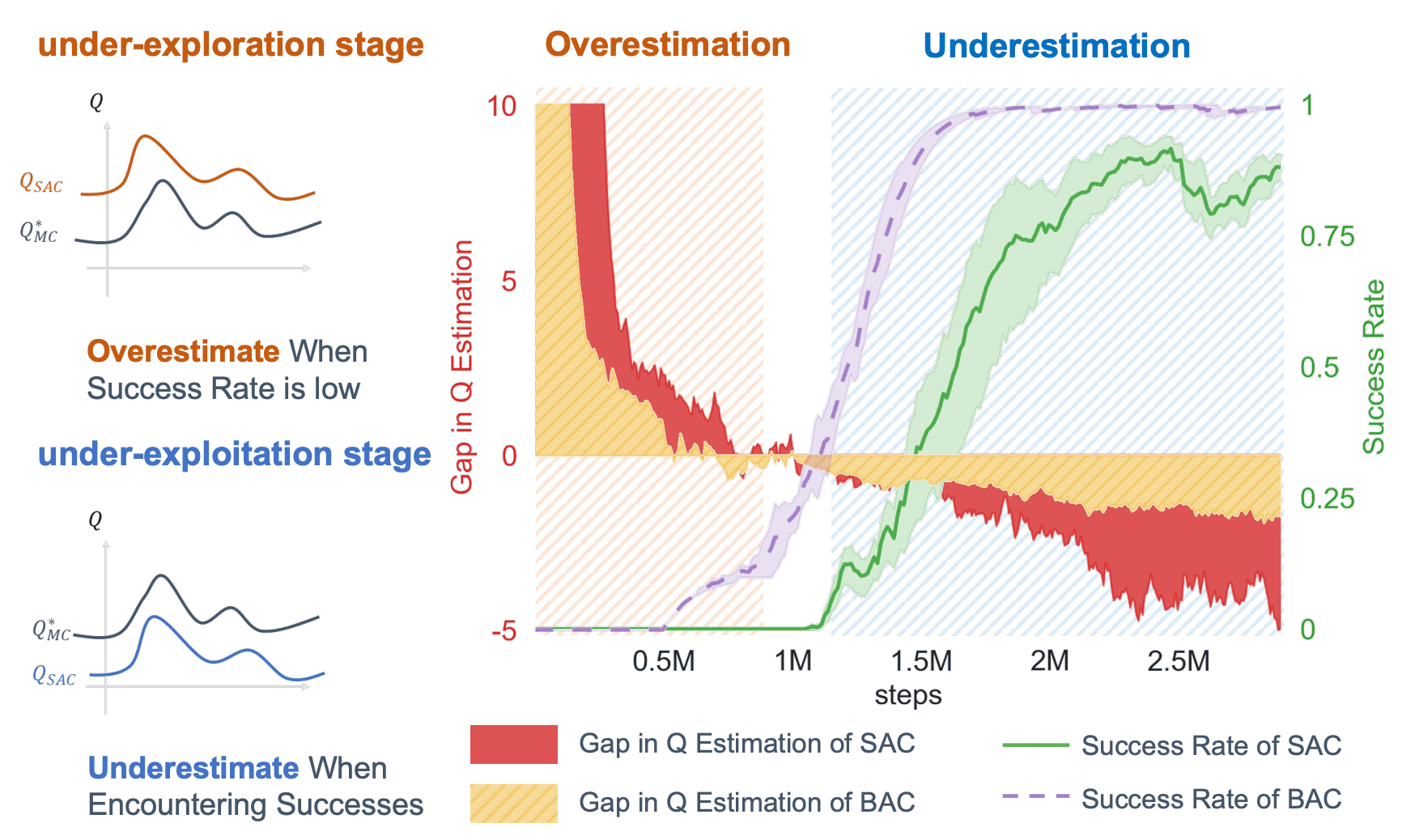
The authors refer to this gap as under and over exploitation stages of the
training. Figure 3 shows that Soft Actor Critic (SAC), a
state of the art off-policy actor critic algorithm, exhibits this gap
consistently across different Mujoco tasks. Figure 3. Visualization of $∆(µ, π)$ across
four different tasks using a SAC agent. Blue bars correspond to positive $∆(µ,
π)$, indicating the “under-exploitation” stage, while orange bars represent the
“under-exploration” stage. [Ji23S]
To address the problem the authors propose an exploitation Bellman operator $\mathcal{T}_{exploit}$ with Bellman target:
$$ \mathcal{T}_{exploit} \ Q_\theta(s,a) :=r + \gamma \max_{a’ \in A(s,\pi_\beta)} Q_{\hat{\theta}}(s’,a’) , $$
where $A(s,\pi_\mu) = \{a \in A | \mu(a|s)>0\}$ is the supported set of actions of all past policies for state $s$ in the replay buffer $D$.
To obtain the final training objective of the critic, a new Bellman operator, the blended exploitation and exploration (BEE) operator, is defined as:
$$ \mathcal{T}_{BEE} = \alpha \mathcal{T}_{exploit} + (1-\alpha) \mathcal{T}_{explore}. $$
The resulting actor critic algorithm using the BEE operator is referred to as blended actor critic (BAC).
The Algorithm
Running the BEE operator requires the choice of exploration and exploitation operator. The authors suggest an implementation based on SAC, so the exploration term is the entropy of the policy. A possible algorithmic instantiation of the exploitation Bellman operator leverages expectile regression which (as well as the stabilising Q-V decomposition) is also used in implicit Q-learning see our previous paper pill.
Predicting an upper expectile of the TD-target approximates the maximum of $r (s,a) + \gamma Q_\theta(s’,a’)$ over actions $a’$ constrained to the replay buffer actions. The resulting training objective for the critic is:
$$ L_{TD}(\theta) = \mathbb{E}_{(s,a,r,s’) \sim D} \left[\left(r + \gamma \max_{a’ \in A(s,\pi_\beta)} Q_{\hat{\theta}}(s’,a’) - Q_{\theta}(s,a) \right)^2\right], $$
where $A(s,\pi_\beta) = \{a \in A | \pi_\beta(a|s)>0\}$ is the supported
set of action of policy $\pi_\beta$ for state $s$ via replay buffer $D$. Using
expectile regression ensures that the Bellman target is not impacted by
potentially suboptimal performance of the current policy.
Even so only actions in the support of the buffer are considered, the
objective also incorporates stochasticity that comes from the environment
dynamics $s’ \sim P(·|s, a)$. Therefore, a large target value might not
necessarily reflect the existence of a single action that achieves that
value, but rather a “fortunate” sample transitioning into a good state. The
proposed solution is to introduce a separate value function $V_\psi$
approximating an expectile purely with respect to the action distribution.
This leads to the final training objective for the value function:
$$ L_V(\psi) = \mathbb{E}_{(s,a) \sim D} [L_\tau^2 (Q_{\hat{θ}}(s,a) − V_\psi (s))]. $$
This value function is also used to train the Q-functions with MSE loss, averaging over the stochasticity from the transitions and avoiding the aforementioned “lucky” sample issue:
$$ L_Q(\theta)=\mathbb{E}_{(s,a,s′) \sim D}[(r(s,a)+γV_ψ(s′)−Q_\theta(s,a))^2]. $$
Experimental Results
In addition to the “standard” Mujoco experiments that show superior performance of the BEE operator, the authors consider Kitty robotics experiments. D’Kitty is a quadruped robot traversing various complex terrains towards a goal position. Reward components include reaching the goal and standing upright. The experiments follow the typical sim2real procedure of pretraining the agent in simulation using domain randomisation on various terrains with subsequent deployment to a test environment. The base task is generated with obstacles of height up to 0.05m. The “DKittyWalk-Medium” task distribution has obstacles of height up to 0.07m and the “DKittyWalk-Hard” tasks of up to 0.09m.
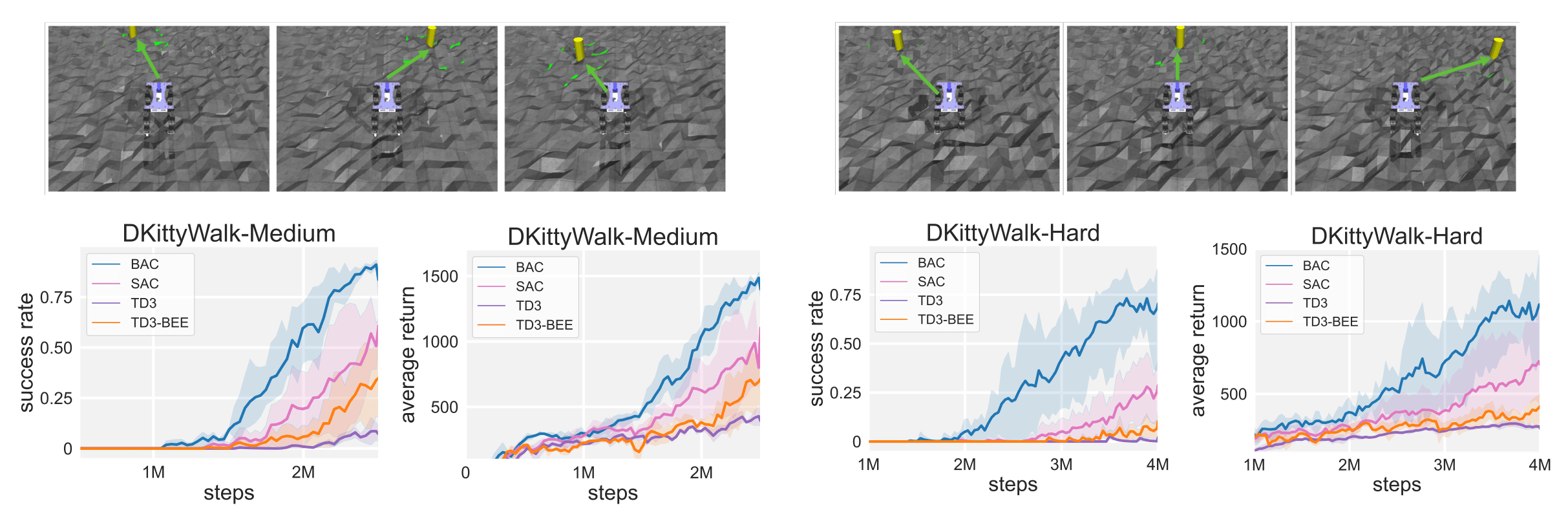
Figure 4. (Left) Success rate and average return in the “DKittyWalk-Medium” task. (Right) Success rate and average return in the “DKittyWalk-Hard” task. [Ji23S]
Figure 5 shows the performance obtained when deploying the simulation trained policy with BEE on the real twelve-DOF quadruped robot. The experiment was performed in four different terrains: smooth road (with a target point at 3m), rough stone road (target point at 1m), uphill stone road (target point at 1m), and grassland (target point at 1m).
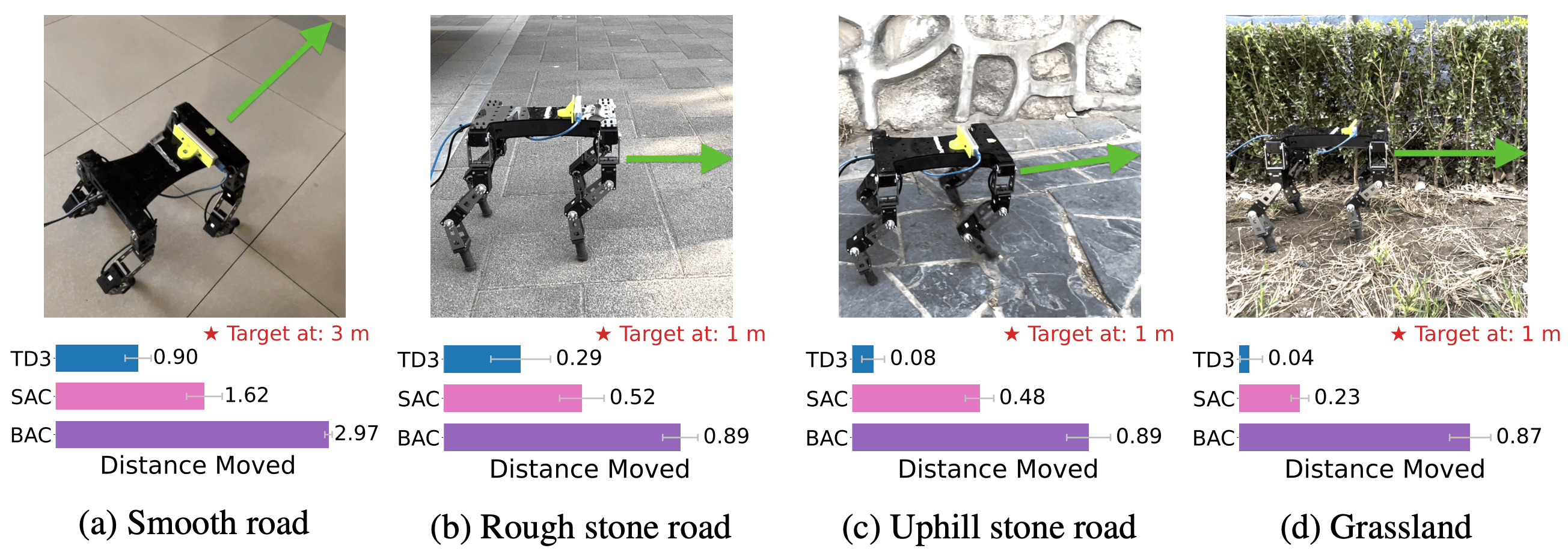
Figure 5. Comparisons on four challenging real-world tasks. The bar plots show how far the agent walks toward the goal for each algorithm averaged over five runs. For (a) and (b), we employ the policy trained in the “-Medium” task, and for (c) and (d) use the policy trained in the “-Hard” task. [Ji23S]
In addition to value-based methods, the authors also propose to integrate the BEE Bellman operator into a dyna-style model based architecture. Notably, they train the exploration operator on the synthetic data from the model rollouts and the exploitation operator on the real world data. For full details as well as more choices for the exploration term $\omega(s’, a’| \pi)$ and in-sample exploitation objective, we recommend to take a look into the paper.
Discussion
Deep RL is famous for things that one wouldn’t expect to go wrong going wrong. The value gap between the historically best behavior and the current policy is one such thing. Bringing insights from designing pure exploitation operators back to the online setting is a promising avenue. While conservative Q-learning can readily be run in an online setting, BEE with expectile regression as exploitation operator can be seen as a generalised online version of implicit Q-learning.
The ablations show another neat property of the BEE Bellman operator.
SAC and BAC are both similarly initialised and provided 15 expert
trajectories (2400 transitions) as replay buffer. Figure 6. Comparison
of the ability to seize
serendipity in the “DKittyWalk-Medium” task.
Left: success rate; Right: average return.
[Ji23S]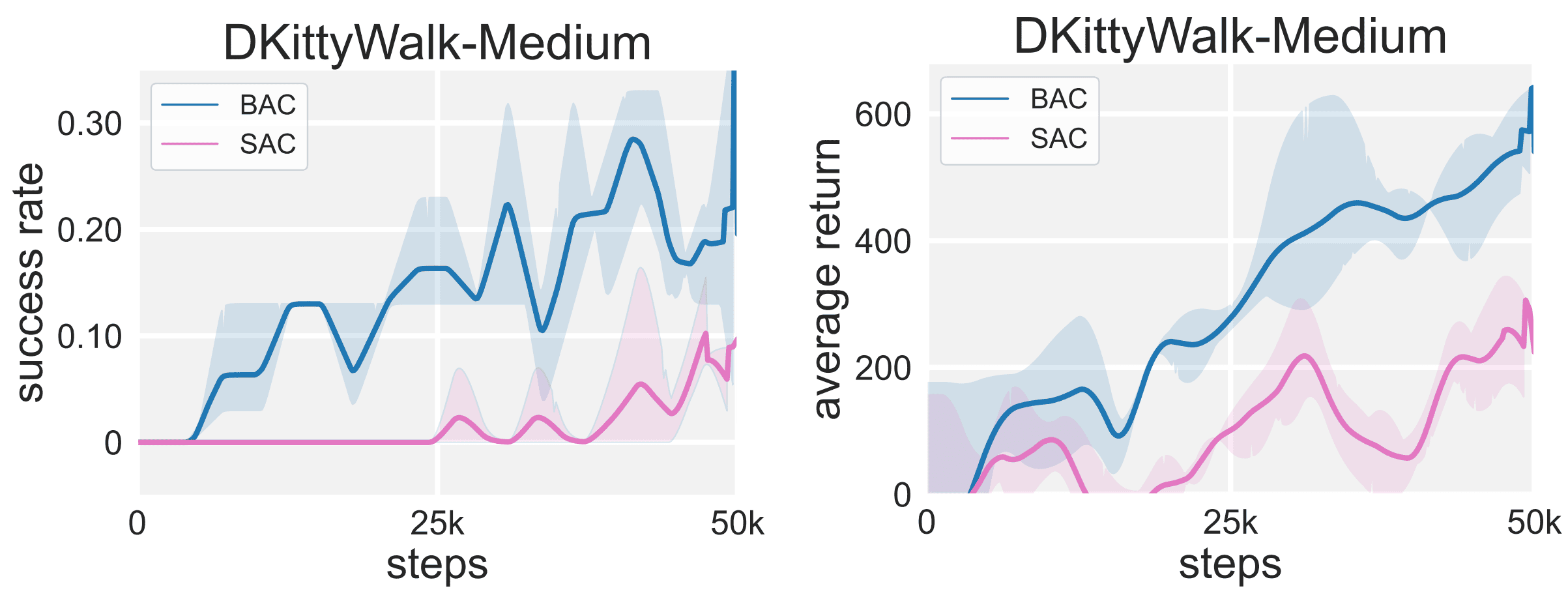
The learning curves clearly indicate the accelerated ability of the BEE Bellman operator to exploit prior knowledge, thus providing an alternative to the common pretraining - online fine-tuning paradigm to incorporate prior knowledge in the form of expert trajectories. An interesting experiment (which was not yet performed) would have been to jumpstart the training with offline data of mixed quality and trajectories that require stitching.