Diffusion models are generative models where training samples are gradually perturbed towards a tractable distribution (typically, a homogeneous gaussian), while a neural network is trained to revert the process and remove the noise. This can be shown to be an effective generative process, able to create never-before-seen data samples from completely random noise.
Current score based diffusion models employ very simplistic diffusions kernels, leading to unnecessarily complex de-noising processes. The seminal paper [Son21S], which we presented in a previous paper pill, showed that the de-noising task that needs to be learned by the neural network is uniquely determined by the forward diffusion process. Hence, the choice of a better forward diffusion process is crucial in obtaining fast and sample efficient generative models.
Based on connections to statistical mechanics, [Doc22S] proposes a novel critically-damped Langevin diffusion model which, for similar model architecture and sampling compute budgets, outperforms the sampling quality of previous models and sets itself as the new state of the art.
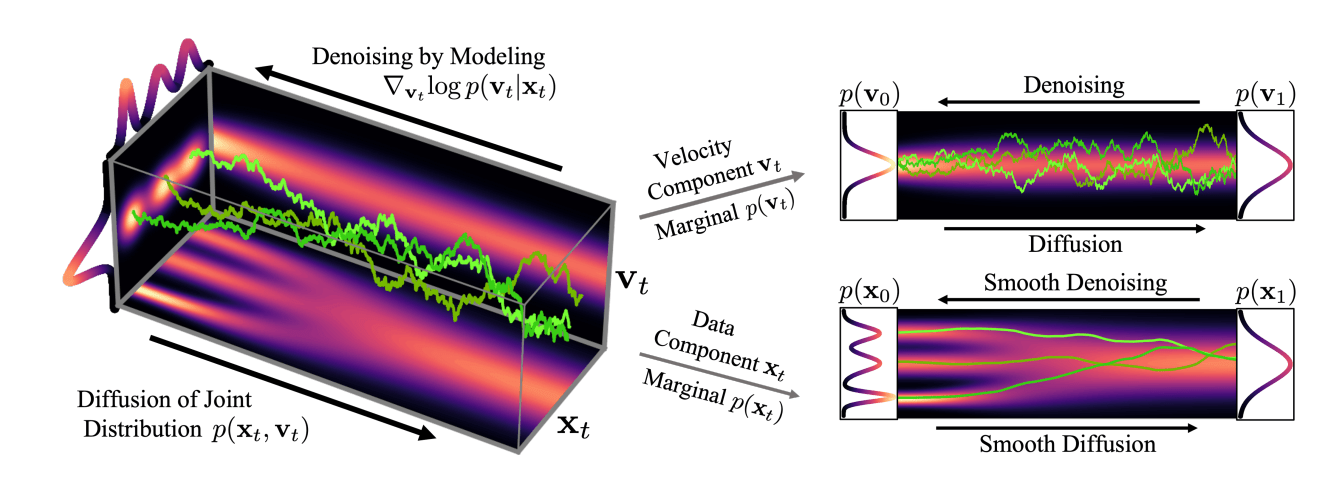
While the paper is rather technical, the main idea is simple: a novel forward diffusion process where the data point variable is augmented by an additional velocity variable and the diffusion process is run in the joint data-velocity space. The two spaces are coupled as in Hamiltonian dynamics, with noise injected only in the velocity space.
In other words, instead of predicting what the point should look like in the de-noised image, the model learns how much each pixel should be changed at each instant of the de-noising process. Since the noise is applied only to such “velocity”, the convergence on the non-velocity (the actual data) dimension ends up being much smoother, as represented in the image above.
Inspired by methods used in statistical mechanics, this work provides new insights into de-noising diffusion models and implies promising directions for future research. Code is available on github, while more info can be found on the group’s website.