Segregation is a concept from social science which describes a tendency of a group with members of mixed types to separate out into clusters of homogeneous types. Segregation is an observable phenomenon in many areas of high social relevance. For instance, Shelling was the first to model the phenomenon of segregation in residential areas in game theoretic terms [Sch69M]. Within his stylized model of social interaction he was able to show that segregation can appear even if there is very little homophile among the members the group (see here for a nice demonstration).

Networks have become even more present in today’s world and many of them are created by decentralized processes driven by some kind of agents. Power networks and the internet are only two examples. With modern technology, the possibilities to design the rules of a decentralized network creation process are more flexible than ever before. Hence, the question arises whether one can design processes with most favorable outcomes for the participants. The IJCAI 2022 paper [Bul22N] provides additional understanding of segregation phenomena in network creation games (see below) and first hints on how to circumvent segregation.

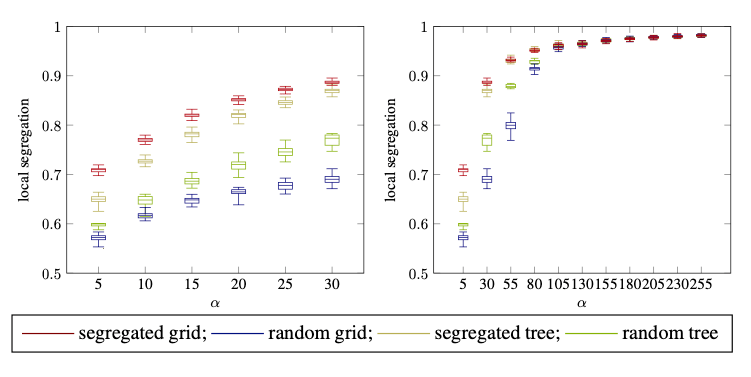Local segregation under NCG-ICF with different initializations and alpha values (with and without deleting edges). Since the pioneering work in the 1970s there has been much follow-up research (see e.g. [Elk19S]). Most of the early work was empirical in nature but more recently the game theory community has begun to take a more principled look into the phenomenon. A popular model of network creation are network creation games (NCGs). Selfish agents establish connections to other agents in order to balance the costs of establishing a connection against a desire to be central in the network (expressed as a penalty that is equal to the summed distances to all other nodes in the network).

To better understand the causes of segregation, the authors initiate the study of heterogenous NCGs. In this variant agents have one of finitely many types. They use additional penalties to separately investigate two possible causes for segregation. In both cases the use fixed base edge costs with an additional additive penalty term that can be either described as homophilic (increasing comfort among friends penalty, ICF) or prejudiced (Decreasing effort of integration penalty, DEI). In both cases the edge costs are multiplied by a parameter alpha which is used to scale them against the centrality penalty.

The authors investigate the segregation level of stable networks (no agent can gain from deleting an edge and no pair of agents can both profit from creating an edge between them) under the two versions of NCG. Somewhat surprisingly, they find a very similar behavior under ICF and DEI. For alpha slightly smaller than one, stable networks are guaranteed to have small diameter and low segregation. For alpha close to one there is provably high segregation for every stable network. Finally, for alpha values slightly larger than one, the analysis shows that stable networks can have a large spectrum of segregation levels. This is actually good news since it means that only for a small bandwidth of the parameter alpha high segregation is unavoidable. Hence, there is hope that we can find ways to make stable networks with low segregation more likely as outcome. 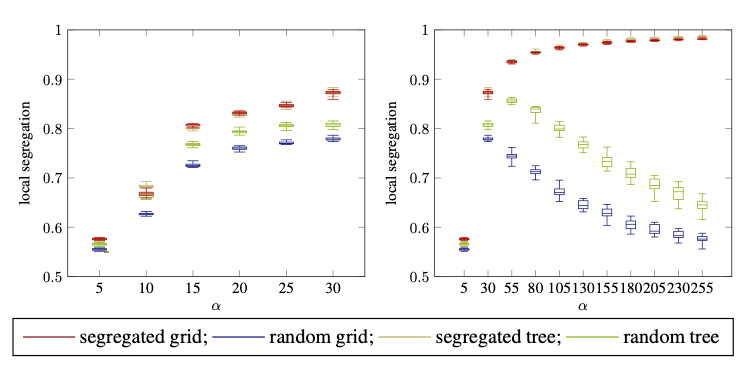Local segregation under NCG-ICF with different initializations and alpha values (with and without deleting edges).

To get a better intuition for alpha larger than one, the authors conduct simulation studies of the game (with and without edge deletions) under different initial conditions, assuming that every agent plays their best response. An important observation is that the initial conditions seem to play an important role, especially for the DEI penalty. Segregation is very unfavorable in many real world scenarios. Although network creation games are highly stylized versions of real processes, and it is not quite clear how well the results are transferable to real world scenarios, the analysis still hints to a possible escape route from segregation through initial integration investments.

To get a better intuition for alpha lager than one, the authors conduct simulation studies of the game (with and without edge deletions) under different initial conditions, assuming that every agent plays his best response. An important observation is that the initial conditions seem to play an important role, especially for the DEI penalty. Segregation is very unfavorable in many real world scenarios. Although network creation games are highly stylized versions of real processes, and it is not quite clear how well the results are transferable to real world scenarios, the analysis still hints to a possible escape route from segregation through initial integration investments.