Uncertainty estimation is a crucial part of reliable deep learning applications and Bayesian Methods are a natural fit for this task. In a previous pill we already discussed the possibility of approximating the posterior of the network weights and sampling from it to obtain uncertainty estimates. [Cha22N], accepted at ICLR22, explores another interesting path starting with the premise that one would like to approximate the prediction uncertainty given the input observation with a distribution from the exponential family.
The exponential family is a flexible family of distributions that provides reasonable distributions for classification (categorical), regression (e.g. Gaussian), or count prediction (e.g. Poisson). They use that every distribution in the exponential family has a conjugate prior on its natural parameters that can be expressed in terms of two parameters, a vector $c$ and a number $n$. The parameters of the prior are connected to the decomposition of the predictive uncertainty into aleatoric and epistemic components, i.e. into the irreducible uncertainty in the probabilistic model and the lack of knowledge about the true model. While $c$ carries the aleatoric uncertainty, $n$ aligns well with the epistemic uncertainty.
Inspired by the simple closed form solution for the posterior distribution of the parameters, the authors consider a similar update procedure to compute the posterior distribution of the parameters given the input features, i.e. for point-wise Bayesian posterior updates. They do so by employing a neural pipeline. Specifically, the data is mapped to a low dimensional space, a normalising flow is used for density estimation in the latent space, and a regressor is trained to compute the updated value of $c$. The density estimation is used to compute the updated parameter $n$, where lower values are assigned low density regions. The Bayesian update is then performed as if the update parameter were obtained from observations of the target variable. Hence, the approach can be understood as translating the input into pseudo-observations of the target variable.
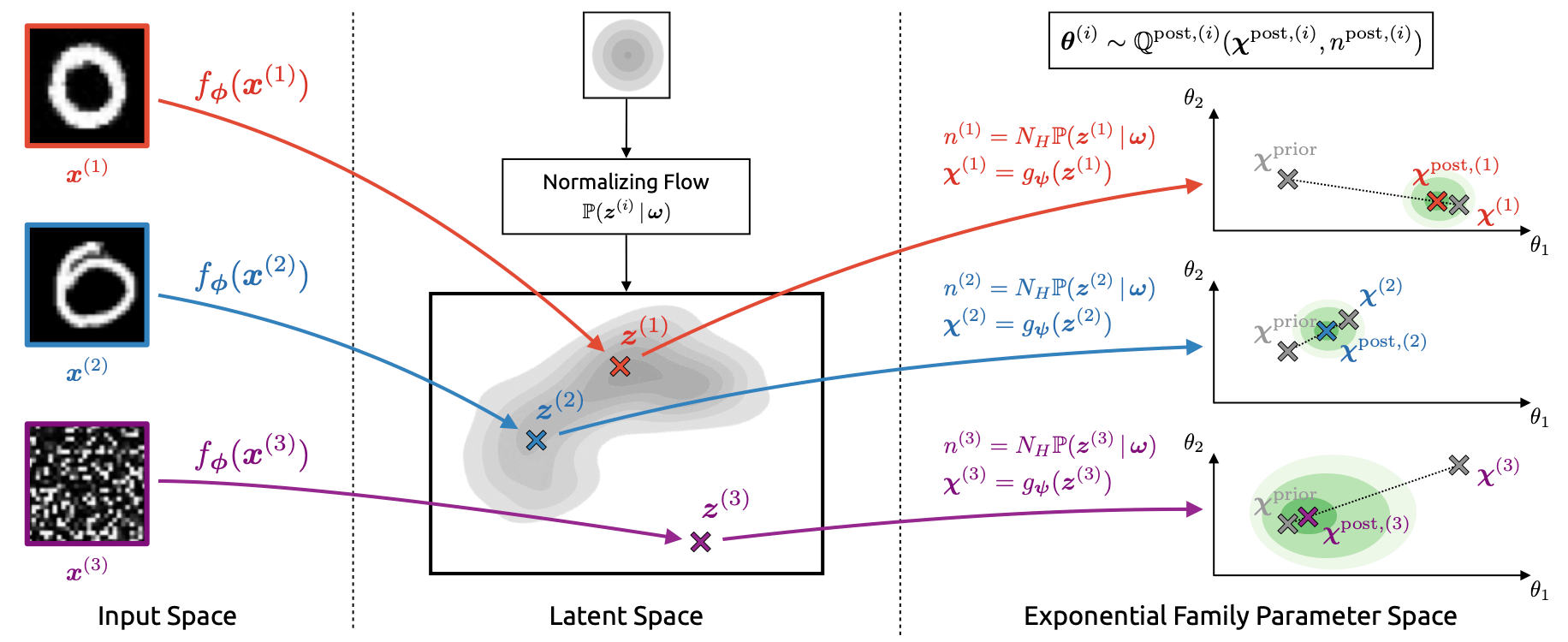
Figure 2: Overview of Natural Posterior Network. Inputs $x^{(i)}$ are first mapped to a low-dimensional latent representation $z^{(i)}$ by the encoder $f_\phi.$ From $z^{(i)}$, the decoder $g_\psi$ derives the parameter update $\chi^{(i)}$ while a normalizing flow $\mathbb{P}_\omega$ yields the evidence update $n^{(i)}$. Posterior parameters are obtained from a weighted combination of prior and update parameters according to $n^{\operatorname{post},(i)}.$
The entire system is trained using the Bayesian loss which is the sum of the expected log-likelihood of the data under the posterior with an entropy regulariser. Interestingly, this loss turns out to differ in the continuous case from the popular KL-loss.
The authors perform extensive experiments for different tasks such as classification, regression, count prediction, and anomaly detection. They show that their approach is highly competitive against SOTA methods across all of them.
Altogether, this seems to be a simple but effective Bayesian uncertainty estimation method.