Minimax optimization has found multiple applications in machine learning. The training of generative adversarial networks or robust reinforcement learning are only two of them. However, these applications often lead to nonconvex-nonconcave minimax objectives which cause notorious problems for first-order methods. There is a rich literature that witnesses failures of first-order methods such as divergence or cyclic behavior of the optimization procedure.
Traditionally, minimax optimization problems have been studied under the umbrella of variational inequalities (VIs). In short, VIs are a uniform representation of a wide range of optimization problems. A survey can be found here. The difficulty in the nonconvex-nonconcave case has been established in terms of exponential lower bounds of classical optimization type and in terms of computational complexity.
A classical approach to guarantee convergence outside the convex-concave setting is to assume some additional structure in the problem formulation. One important case are Minty variational inequalities (MVI) which include all quasiconvex-concave and starconvex-concave problems.
Last year, Diakonikolas proposed a relaxation of MVI, called weak Minty variational inequality, by adding a new parameter to the formulation. More precisely, they allow that MVI also admits negative values up to a certain range that is governed by the parameter. They also developed an extension of the classical extra gradient algorithm, called EG+ and showed that for a certain range of the new parameter EG+ converges to a stationary point. However, the new class of problems was still too weak to capture even the simplest known counterexample for general Robbins-Monro first-order schemes (the forsaken example, see here).
The paper [Pet22E] proposes curvatureEG+, an extension of the EG+ algorithm. The main difference to EG+ is the adaptive computation of the step size. They show that curvatureEG+ converges for a broader range of the parameter in the weak MVI definition than EG+. Interestingly, this is enough to capture the aforementioned forsaken example (see below).
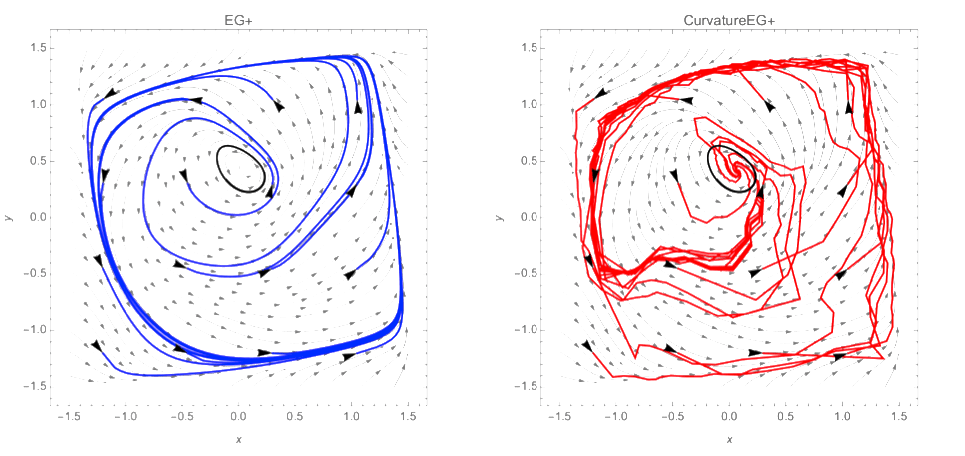
Figure 1: Forsaken (Hsieh et al., 2021, Example 5.2) provides an example where the weak MVI constant ρ does not satisfy algorithmic requirements of (EG+) and (EG+) does not converge to a stationary point but rather the attracting limit cycle (left). In contrast, adaptively choosing the extrapolation stepsize large enough with our new method, called (CurvatureEG+), is sufficient for avoiding the limit cycles (right). The repellant limit cycle is indicated in black and the stream plot shows the vectorfield Fz. The blue and red curves indicate multiple trajectories of the algorithms starting from initializations indicated in black.
Minimax optimization has just recently entered the stage in machine learning, and I am delighted to see how this new domain of application already sparks new impulses for this complex but important topic.