The transformer architecture has been very influential in many application areas of machine learning such as natural language processing and computer vision. It replaces computations along the structure of the input by a fully connected message passing scheme. This idea seems to be perfect to tackle the inherent limitations of local message passing on graphs as it is usually performed by graph neural networks. However, in order to make the structure of the input available to the networks, one needs to add positional encodings to the node features. This is a problem since there is no canonical way of ordering the nodes of a graph.

Still, there is a natural analogy between the sine and cosine based positional encoding on linear structures such as text and the eigenvectors and eigenvalues of the graph Laplacian: They can be interpreted as the frequencies of resonance of a graph (see [Van03W] for some background on this matter).

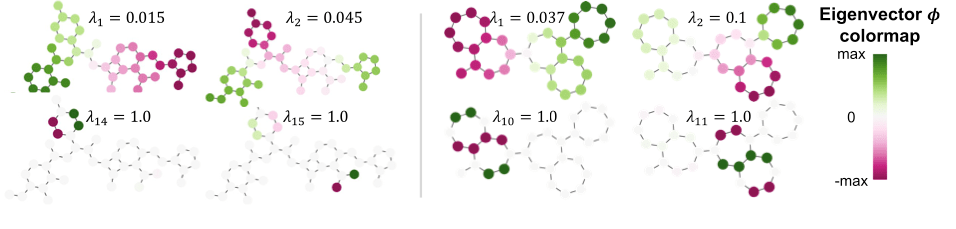
[Kre21R] proposes to use the laplacian eigenvectors of a graph as basis for the positional encoding. While this is not the first work to propose this idea, they are the first to handle the inherent sign ambiguity in the eigenvector selection (see [Vel20G][Dwi21G] for prior work). Also, they are the first one to obtain good experimental results with global attention on graphs.