Generative graph models have gone long beyond Erdős–Rényi or Kronecker graphs. With increasing complexity, the need for powerful methods to evaluate and compare generative graph models arises. The ICLR paper [Obr22E] investigates common practices to compare graph distributions with some sobering results.
The major obstacle to define divergences in a similar way as it has been done for distributions over vectors is that graphs can be of different sizes, and they are only specified up to isomorphism, i.e. one graph can be represented by multiple adjacency matrices. The research community has largely adopted maximum mean discrepancy (MMD) as the standard approach. MMD is a general technique to compare distributions over structured objects that works according to the following schema:
- Choose a function that maps graphs into some real-valued vector space.
- Choose a kernel on the vector space.
- Apply the function to samples of the two distributions.
- Obtain an unbiased estimate of the MMD by taking the average pairwise similarity between the vectors of the two classes w.r.t. the kernel.
While MMD is a very powerful and versatile method, it comes with many pitfalls when used to compare graph distributions. The authors survey the recent literature considering how MMD is performed in practice and find some major problems. Their findings can be summarised as follows:
- Function, kernel, and hyperparameters are often chosen without considering the true distribution (that we wish to estimate).
- Sometimes, non-positive semi-definite functions are chosen as kernels, breaking all theoretical guarantees for MMD.
Additionally, they conduct experiments and find that the choice of the kernel and also the choice of hyperparameters can arbitrarily change the result of an evaluation. From their findings, they assembled the following guidelines for us:
- Always use proper kernels.
- Choose function, kernel, and hyperparameter based on the samples from the true distribution (avoid dependencies on the model).
- Use perturbations such as random edge or node insertions and deletions to deform the original samples and compute MMD to the original samples. MMD should monotonically increase with the strength of the perturbations. These can be adapted to the specific domain.
Their analysis and recommendations provide useful tools for practitioners wanting to use MMD.
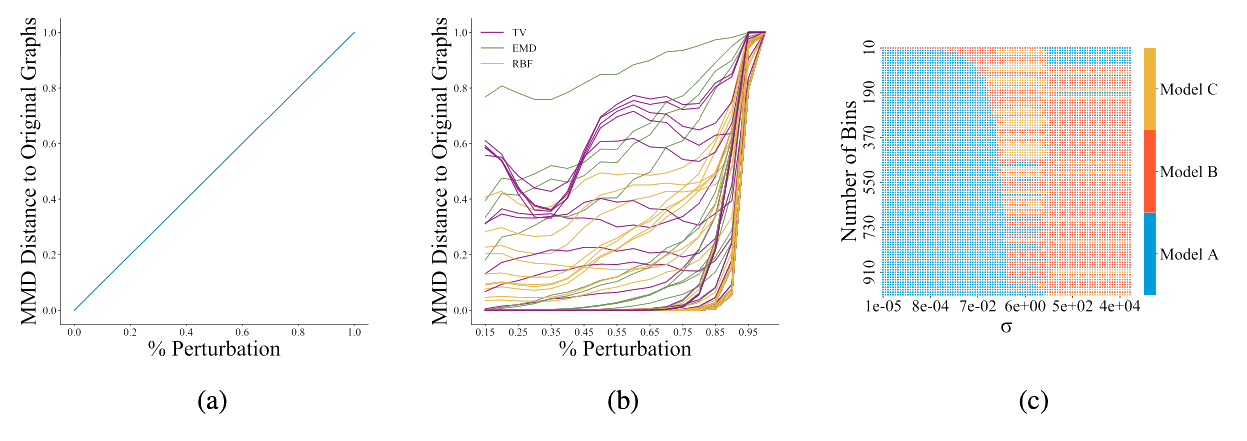
Figure 2: [Obr22E] Figure 2a shows the ideal behaviour of a graph generative model evaluator: as two distributions of graphs become increasingly dissimilar, e.g., via perturbations, the metric should grow proportionally. Figure 2b shows the behaviour of the current choices in reality; each line represents the normalized MMD for a given kernel and parameter combination. A cautious choice of kernel and parameters is needed in order to obtain a metric with behaviour similar to Figure 2a. Each square in Figure 2c shows which model performs best (out of A, B, and C) over a grid of hyperparameter combinations of σ and number of bins in the histogram. Any model can rank first with an appropriate hyperparameter selection, showcasing the sensitivity of MMD to the hyperparameter choice.