It is not frequent to come across a recent paper that gives new insights on a century-old topic. In my opinion, the outstanding-paper-award winning contribution to ICLR22 [Zha22C] is of this type. In this work, the authors tackle the task of designing a metric over probability distributions that can be tailored to a user’s particular interests and can be estimated efficiently from samples.
Measuring differences between distributions in a meaningful way is not simple. For example, slight misalignment between discrete distributions might produce a large difference according to some metrics (like KL-divergence) and a small one according to others (like Wasserstein metric).
In the paper mentioned above, the design of the new class of divergences has its roots in statistical decision theory and is based on the H-Entropy, a notion introduced in 1962 [Deg62U]. For an arbitrary action space $\cal{A}$ (which can be infinite dimensional), a probability measure $p$ over $\cal{X}$, and a loss function $\ell: \cal{X} \times \cal{A} \rightarrow \mathbb{R} $, the H-Entropy of $p$ is the infimum w.r.t. actions in $\cal{A}$ of the expectation of the loss under $p$:
$$ H_\ell(p) = \inf_{a \in \cal {A}} \mathbb{E}_p [ \ell(X, a)] $$
In other words:
H-entropy is the Bayes optimal loss of a decision maker who must select some action $a$ not for a particular $x$, but in expectation for a random $x$ drawn from $p$.
Now one proceeds with the following intuition: given two different probability distributions $p$ and $q$, the optimal action on their mixture, $(p + q)/2$, will result in a larger loss than losses of the optimal actions on $p$ or on $q$ individually. Thus, the difference between the H-entropy of the mixture and the H-entropies of the components gives a measure of how different $p$ and $q$ are from each other in the context of decision-making for a selected set of actions and loss function. From this intuition, the definition of the new H-divergence naturally follows, as per the following:
Definition 2 (H-divergence, [Zha22C]). For two distributions $p,q$ on $\cal{X}$, given any continuous function $\phi:\mathbb{R}^2 \rightarrow \mathbb{R}$ such that $\phi(\theta,\lambda) \gt 0 $ whenever $\theta + \lambda \gt 0$ and $\phi(0,0)=0$, define
$$D^\phi_\ell(p||q) = \phi\left(H_\ell\left(\frac{p+q}{2}\right)-H_\ell(p), H_\ell\left(\frac{p+q}{2}\right)-H_\ell(q)\right)$$
Intuitively $H_\ell\left(\frac{p+q}{2}\right)-H_\ell(p)$ and $H_\ell\left(\frac{p+q}{2}\right)-H_\ell(q)$ measure how much more difficult it is to mnimize loss on the mixture distribution $(p+q)/2$ than on $p$ and $q$ respectively. $\phi$ is [in] a general class of functions that map these differences into a scalar divergence(…)
In addition, the authors define an efficient estimator for H-divergences from finite samples.
This new concept has many applications. Selecting a loss and action space suitable to the domain of interest results in powerful hypothesis-testing tools. Moreover, this specialization to a domain allows not just to compare probability distributions but to assess how much impact the difference between them has on one’s own decision-making processes. The authors applied H-divergence to the analysis of how changes in weather due to climate change affect different economical decisions (see image below).
Overall, the paper is very well written and contains a lot of experiments, intuition and clarifications. I really recommend reading it. For me, it also served as motivation to dive deeper into the classical topic of statistical decision theory [Deg05O].
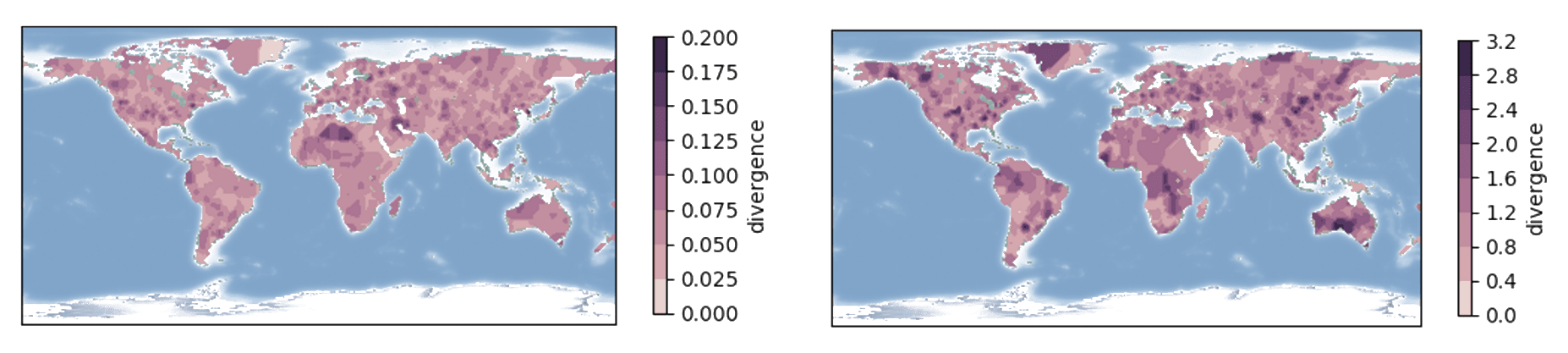
Figure 3: Example plots of H-divergence across different geographical locations for losses $\ell$ related to agriculture (left) and energy production (right). Darker [lighter in dark mode] color indicates larger H-divergence. Compared to divergences such as KL, H-divergence measures changes relevant to different social and economic activities (by selecting appropriate loss functions ℓ). For example, even though climate change significantly impact the high latitude or high altitude areas, this change has less relevance to agriculture (because few agriculture activities are possible in these areas).