The robustness of a neural network classifier is a measure of the stability of its predicted classes against input perturbations. When these are bounded, certification typically proceeds by quantifying how inputs are transformed by the network. Popular techniques include convex relaxations of the worst case error (see our blog post), or layer by layer propagation of interval bounds on the activations (IBP). Because this analysis is made trivial if one knows the Lipschitz constant of the network, some work has been dedicated to controlling and estimating the global Lipschitz constant of networks (and sometimes local constants), but this leads to constrained problems that are costly to solve or bounds that quickly lose sharpness.
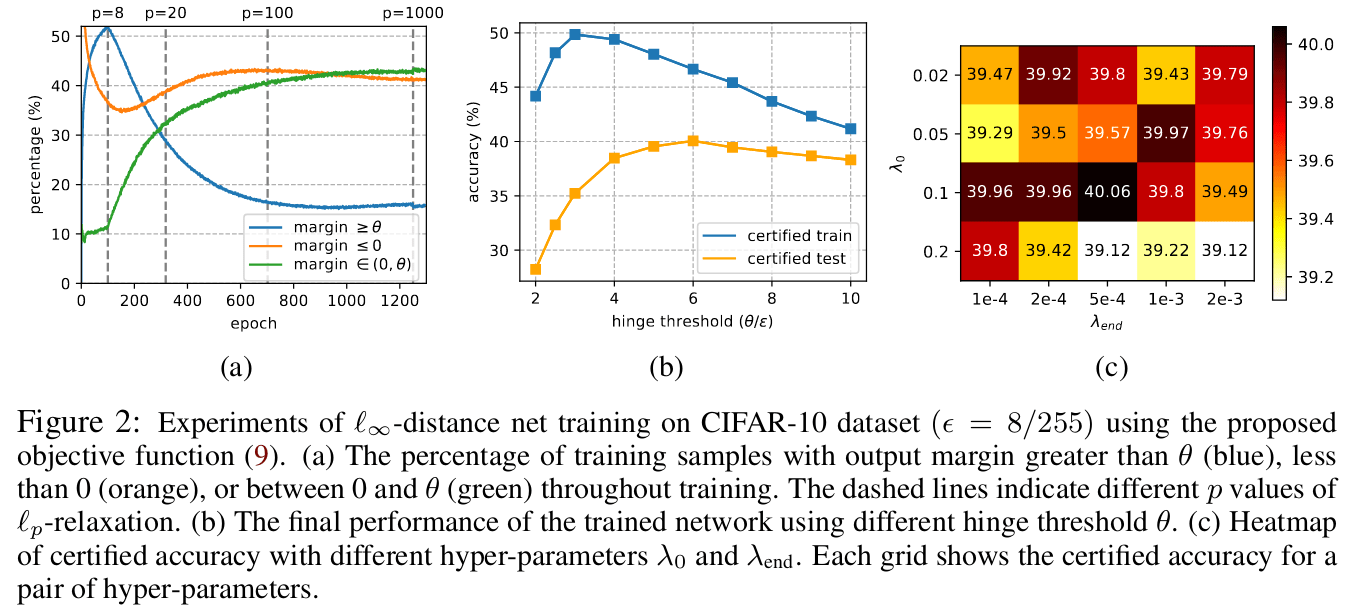
Alternatively one can change the architecture to implicitly control the Lipschitz constant: In “Towards Certifying L-Infinity Robustness Using Neural Networks with L-Inf-Dist Neurons” [Zha21C] the authors change the standard composition of affine map and non-linearity in a neuron to simply the supremum norm of the difference between weights and inputs. This construction has Lipschitz constant 1, providing a built-in robustness certification which depends on the margin between the top predicted confidence and the next one. Because of this, the authors use a hinge loss, but optimization issues arise because of the sparsity of the subdifferential of the supremum norm. Attempts to fix these with L-p relaxations of the neurons (increasing p during training) lead to suboptimal results (seen because most datapoints don’t attain zero loss) and non-robust performance degrades wrt. standard networks.
In the followup paper “Boosting the Certified Robustness of L-infinity Distance Nets” [Zha22B] presented at ICLR 2022, the authors improve over this result. Adding a scaled cross entropy and clipping the hinge loss, the same training procedure increases the number of points with large confidence margins (and hence 0 loss), something that is reflected in a considerable increase in certified robustness, often beating SoTA by many points in CIFAR-10 benchmarks. In the discussion in openreview, the authors mention improvements in harder and larger datasets like TinyImageNet.
Finally, the authors constructively show that under a natural separation condition for data, a shallow L-infinity network of width equal to sample size can achieve perfect 100% robust accuracy. This in contrast to the negative result of “The Fundamental Limits of Interval Arithmetic for Neural Networks” [Mir21F], which proves that IBP cannot achieve perfect certified robustness on separated datasets.
With some improvements, L-infinity networks might soon represent a comparatively cheap alternative for certified robustness.