Diffusion probabilistic models (DPMs) have recently emerged as the state of the art for generative modelling. At their core, they rely on a very simple idea: given a training sample (e.g. an image), one first iteratively and gradually adds gaussian noise (on each pixel) over a series of time steps, and secondly trains a neural network to reverse this process. Removing the noise from the “corrupted” samples, the NN learns to recover the initial image, thus becoming a high quality generative model. So, given a completely noisy image, it can recursively de-noise it towards a brand-new sample, not present in the training set.
Despite their success in sample quality and stability compared to VAEs and GANs, DPMs suffer from very slow inference due to the need to iterate over thousands of samples. One of the key reasons why so many de-noising steps are necessary is related to the estimation of the pixel variance in the reverse (de-noising) process. Previous works have used handcrafted values or trained a separate estimator, e.g. a neural network, thus slowing down training.
[Bao22A] presents the surprising result that the optimal reverse variance of a DPM has an analytic form w.r.t. their score function. This means that, with a fast Monte Carlo based approach, one can increase the efficiency of the backward de-noising process considerably while keeping comparable or even superior performance.
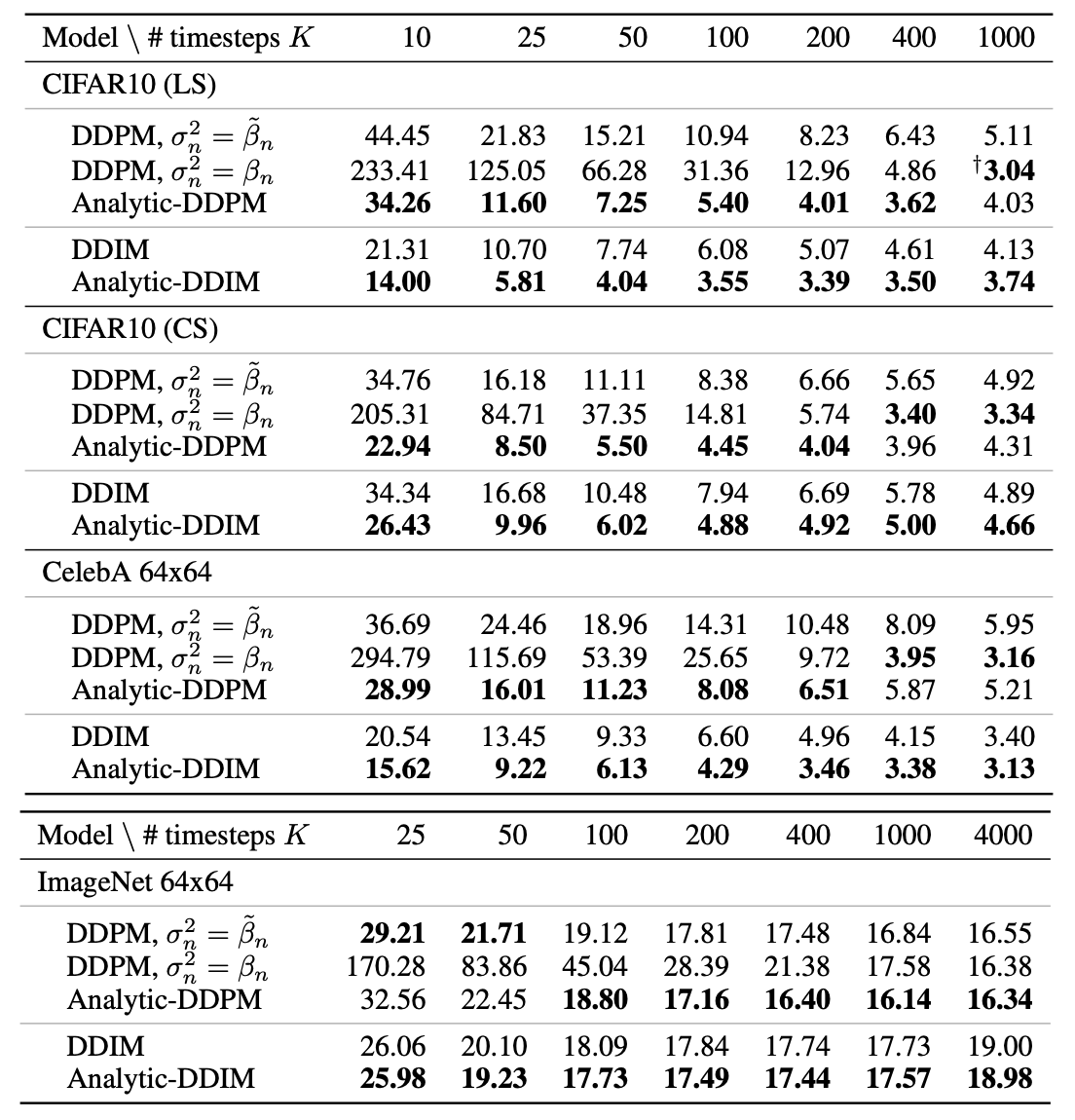
The table above shows the comparison in sample quality using the Frechet Inception Distance (FID) score. Introduced in [Heu18G], the FID score calculates the Wasserstein distance between the distribution of activations for generated and training images in one of the deeper layers of the Inception v3 network. Lower scores (lower distances) have been shown to correlate well with higher quality of generated images.
The newly proposed method, based on optimal-variance calculation, is used in the models Analytic-DDPM and Analytic DDIM. Columns are the number of steps used in inference, and the four sections represent different datasets and/or different noise schedules (how much noise to input at each training time step). The new model consistently improves sample quality when using the same number of inference steps, and, considering also the log-likelihood of the reverse process, it is comparable to the scores of samples created with 20 to 80 times more steps. This result represents a major advancement in sample-efficient image generation using diffusion probabilistic models, which projects them even more as the go-to approach for generative modelling. Code is available at github.