Our team recently attended the 2022 International Conference on Learning Representations (ICLR, 25th to 29th April 2022). A great amount of new research ideas and articles were presented, and we have decided to summarize all those that caught our attention in a series of paper pills.

Paper pills are a way for us to share interesting papers or projects with the TfL community. Each one is a summary of a publication or a piece of software, with a bit of context, short description of methods, main ideas and key results. They are mainly written for practitioners who want a quick overview of the recent developments but do not have the time to delve into too much detail. Nonetheless, if you are a researcher or feel the need to dig deeper, after reading the pill you should find the main article more accessible.

Importantly, we have primarily focused on areas that are interesting for us and for our industry partners, such as data-centric AI, Probabilistic Programming and Explainability. You can find an overview of our main interests in our series page.

Graph Neural Networks

From Understanding over-squashing and bottlenecks on graphs via curvature

Graph neural networks have become very popular recently as they provide superior quality on a wide range of graph related machine learning tasks. This trend can also be seen in the list of accepted papers at ICLR2022. With well over 60 accepted graph related papers there was quite a lot to see. You will find applications to anomaly detection and question answering in the latter sections. In this section we want to highlight two papers that are concerned with more foundational but nevertheless practically important problems in graph machine learning.

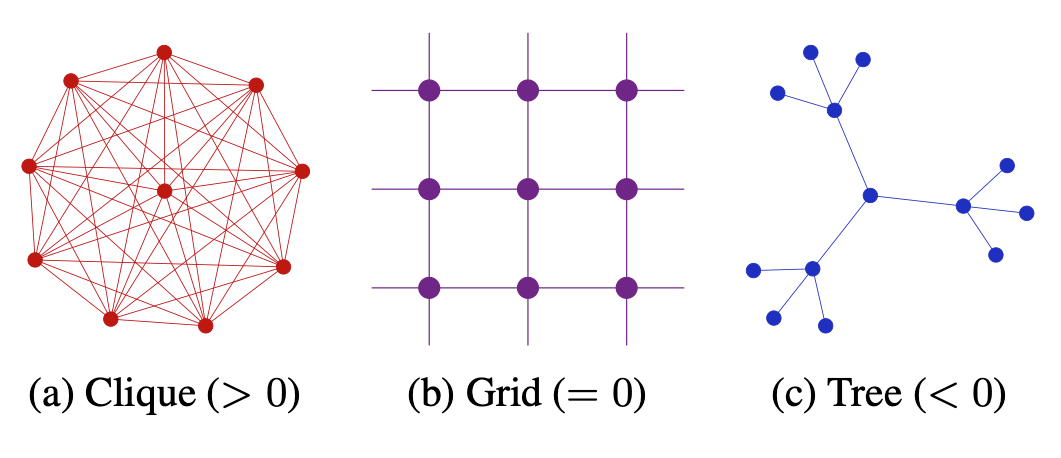
Understanding over-squashing and bottlenecks on graphs via curvature is concerned with the over-squashing phenomenon in graph neural networks. It aims to provide a possible explanation and also develops a method to ease the effect to some extent. Inspired by the Ricci curvature on Riemannian manifolds they define a discrete curvature on graphs. They show that edges with a negative curvature are likely to produce the over-squashing phenomenon and propose a rewiring procedure to eliminate negatively curved edges.

Evaluation Metrics for Graph Generative Models: Problems, Pitfalls, and Practical Solutions critically examines the way we compare graph generative models. The community has largely adopted the maximum mean discrepancy (MMD) as the standard method. To apply MMD one maps graphs generated from both distributions into a vector space via some function $f$ and computes the average pairwise similarity between the graphs of the two distributions with respect to some kernel $K$. While MMD is a very powerful and versatile method, it comes with many pitfalls when used to compare graph distributions. The authors survey the recent literature considering how MMD is performed in practice and find some major problems.

Data Valuation

Shapley values are a concept from collaborative game theory. The goal is to distribute a reward from a collaborative effort fairly among the participants. In the realm of data valuation the concept can be used to attribute the performance of a model to the individual samples in the training data. Unfortunately, the computation of the exact values is often infeasible because it involves fitting a model for all possible subsets of the training data. Improving cooperative game theory-based data valuation via data utility learning proposes to subsample subsets from the power set of the data and only train models for these subsets. The results are used to train a model that predicts the values for the remaining subsets. The authors also provide a theoretical analysis of their approach and show that it can provide a reasonable estimate of the true shapley values while substantially reducing the number of models that have to be fitted.

In our series on data valuation and corresponding library, we analyse this and other methods and their application to common tasks in data science.

Anomaly Detection

From Anomaly Transformer: Time Series Anomaly Detection with Association Discrepancy

Anomaly detection is a challenging topic with many highly relevant industrial applications. It is therefore not surprising to see many anomaly detection papers at ICLR2022. We want to highlight two of them that are concerned with different aspects of anomaly detection on time series.

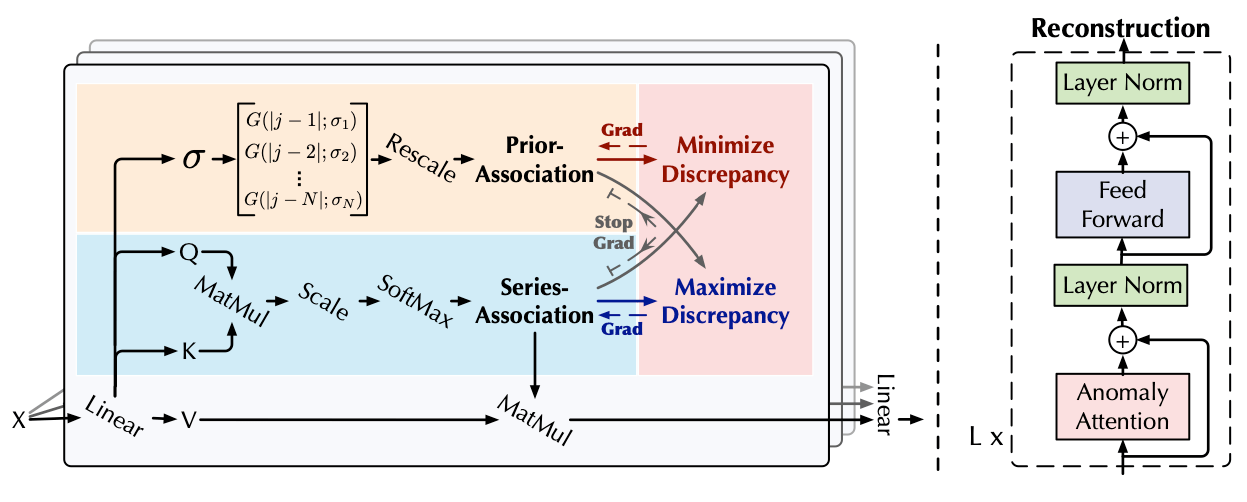
Anomaly Transformer: Time Series Anomaly Detection with Association Discrepancy introduces the concept of association discrepancy. The basic idea is to use a transformer architecture to reconstruct a point in the series from its context through the association weights of the transformer. As usual, one uses the reconstruction loss as anomaly score. However, they want to avoid that the transformer learns to use local associations since anomalies might also be well reconstructed from their local environment, e.g. due to the continuous nature of the underlying data generation process. To achieve this, the associations between the points in time (series association) are trained to increase the symmetrized KL-divergence with respect to a prior association that is based on a Gaussian kernel. The training alternates between adjusting the series association to increase the discrepancy and adjusting the prior association to decrease the discrepancy. This training regime enforces to learn complex non-local associations.

Graph Augmented Normalizing Flows for Anomaly Detection of Multiple Time Series tackles the scenario where one wants to perform anomaly detection on multiple interrelated time series. They also use a reconstruction based approach but use information from all series to reconstruct the points in each individual series. More precisely, they learn a Bayesian network between the time series that represents the interdependencies. To reconstruct a single point in some series, they compute a representation of the history of each series through an RNN. The history representations are then used as features for a GNN that passes messages along the edges of the dependency graph. Finally, the outcome at the node representing the current series is used as input for a conditional normalizing flow that approximates the posterior distribution for the query point given the representation of the history.

Simulation Based Inference

From Variational Methods for Simulation Based Inference

Simulators are an important tool in science and engineering. One of the major difficulties one faces is finding the right parameters that match observations. Often, this has to be done on a fixed dataset of real world experiments. Variational Methods for Simulation Based Inference proposes to use an iterative approach: A surrogate model is trained on observations generated by the simulator with parameters drawn from a prior distribution. Using stochastic variational inference, they compute an approximate posterior distribution for the parameters under the surrogate model given the real world observations and use it as the prior for the next iteration. They demonstrate the effectiveness of the technique on a few very nice examples.

Question Answering

From GreaseLM: Graph REASoning Enhanced Language Models

GreaseLM: Graph REASoning Enhanced Language Models aims to combine two approaches for question answering, fine-tuning large language models and knowledge graphs. While the first learns and stores knowledge about the world implicitly, the latter stores knowledge explicitly in relational triplets. To allow for an interaction between the knowledge graph and the language model, they have a graph neural network processing the relevant part of the knowledge graph in parallel with the computation of the language model. Special interaction nodes and tokens, respectively, allow for a layer-wise interaction between the two models. By applying their techniques to several SOTA pretrained language models they show that their method is able to consistently improve the quality of the answers in comparison with the vanilla fine-tuned language models.

Uncertainty Quantification

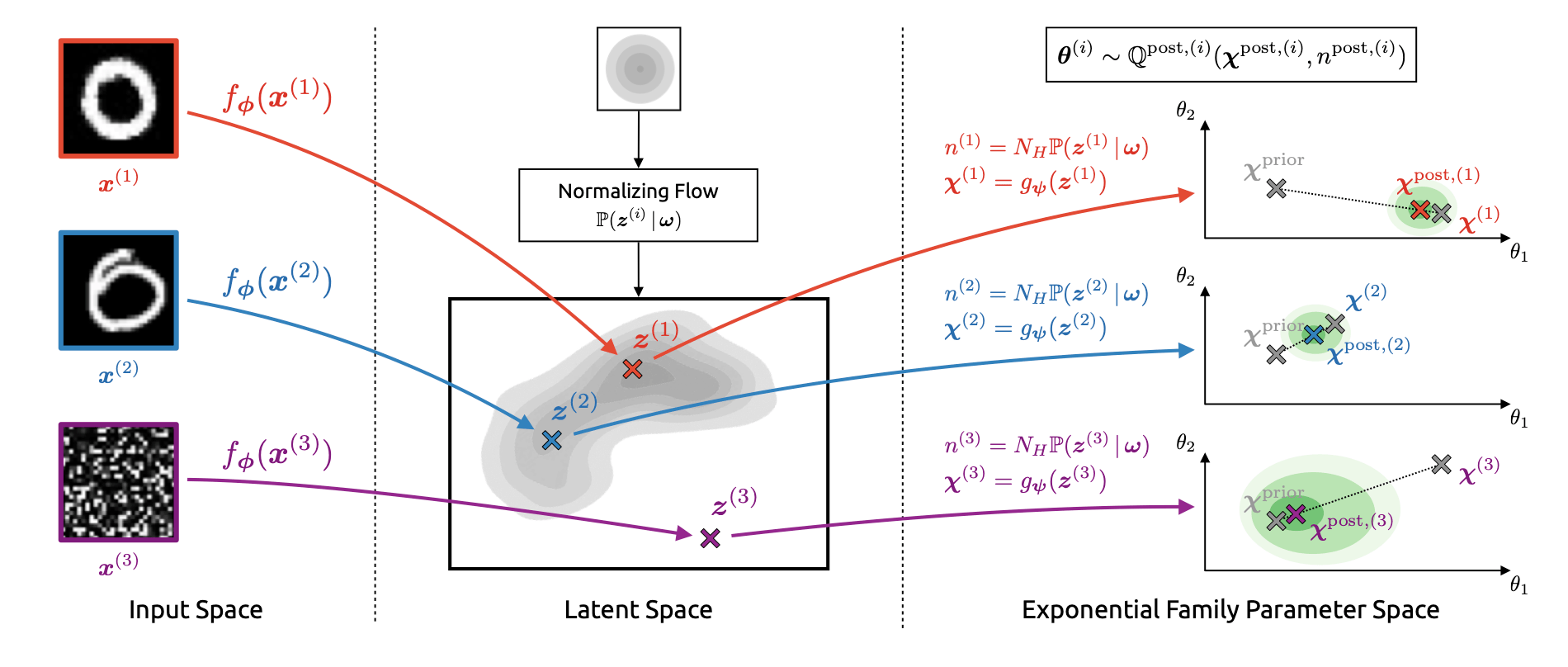
From Natural Posterior Networks

Natural Posterior Networks proposes a method to estimate the uncertainty on the prediction of a neural network with distributions from the exponential family. This is achieved by mapping the input into a low dimensional latent space and using a normalizing flow to map into the parameter space of the exponential family distributions. The authors obtain strong results compared to the baseline methods for various tasks such as classification, regression, count prediction, and anomaly detection.

Minimax Optimization

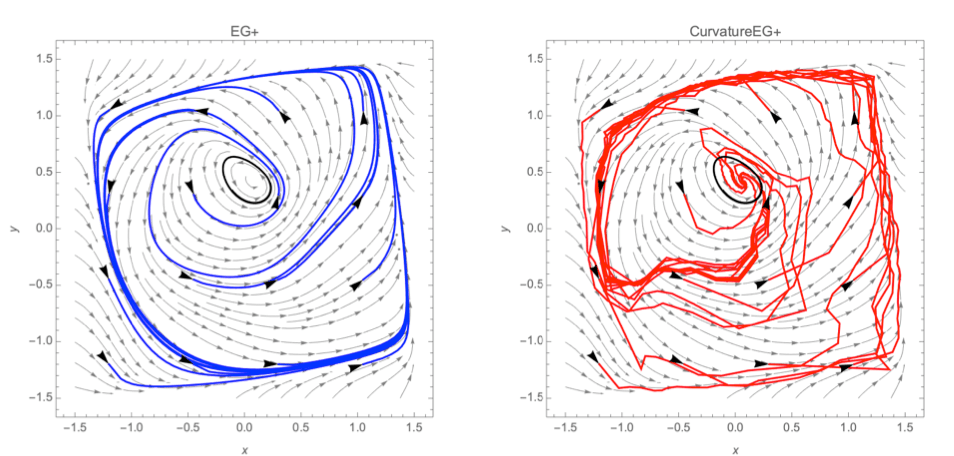
From Escaping limit cycles: Global convergence for constrained nonconvex-nonconcave minimax problems

Minimax optimization has become important for machine learning because of its usage e.g. for training GANs or for the robustness of reinforcement learning agents. However, it is a much more challenging task than ordinary minimization. since first-order methods for optimization can diverge or get trapped in limit cycles. Escaping limit cycles: Global convergence for constrained nonconvex-nonconcave minimax problems builds upon prior work under the umbrella of variational inequalities (VIs, a formalism in which minimax problems can be expressed). They present a new class of VIs and a new algorithm, curvatureEG+, which provides currently the largest class of VIs where an algorithm exists that guarantees convergence. This class is the first one to include known counterexamples where first-order methods fail.

Robustness

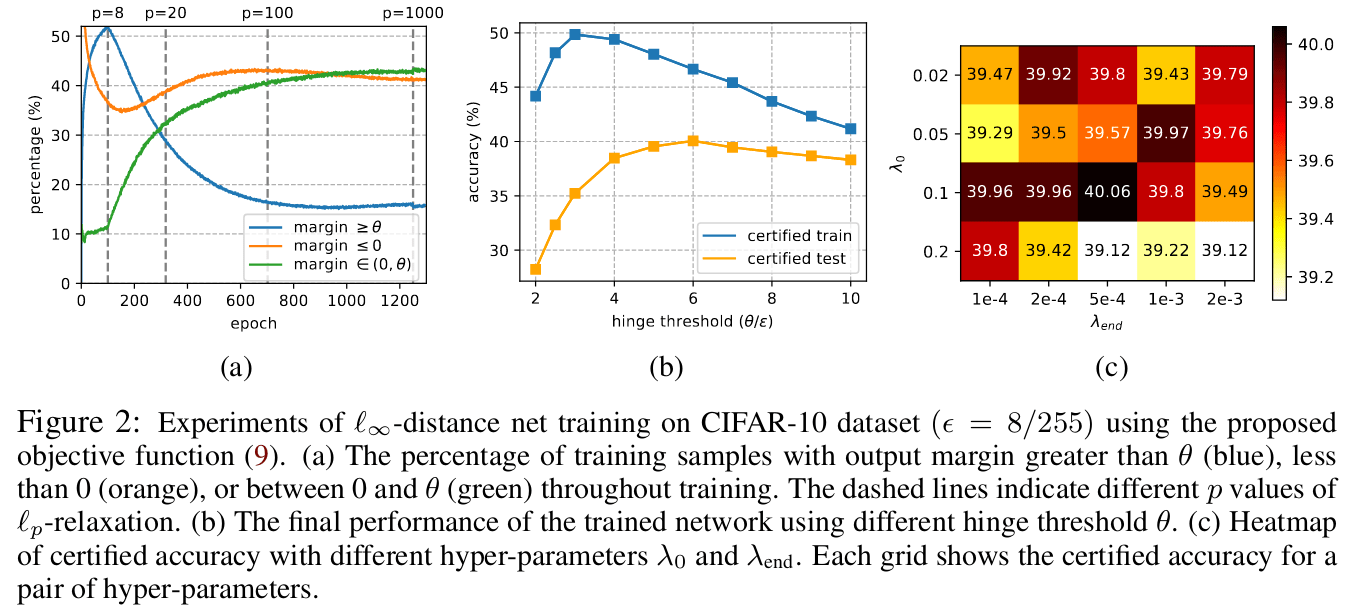From Boosting Certified Robustness of L Infinity Distance Nets

Adversarial robustness measures the stability of a neural network’s predictions against input perturbations. Typically, this happens by quantifying how the inputs are transformed by the network, e.g. through bounds on its Lipschitz constant. L-infinity distance nets are a type of network architecture that is guaranteed to have a Lipschitz constant of 1, but whose training often leads to suboptimal performance. Boosting Certified Robustness of L Infinity Distance Nets proposes some modifications to the loss function of such L-infinity distance nets that lead to a much improved performance.

Distribution shift indicates a phenomenon where the data distribution of a model at training is different from the distribution at inference. Since empirical risk minimization does not provide any guarantees in such a scenario, it is important to apply additional methods to make the model more robust against it, such as data augmentation, resampling, or generating synthetic training samples. A Fine-Grained Analysis on Distribution Shift conducts an extensive experimental study on common methods in computer vision. Along these lines, they introduce a framework for generating distribution shift in a controlled way.

Modelling long sequences with state spaces

Modeling Long Sequences with Structured State Spaces builds on ideas of using state-spaces and linear ODEs in optimal control by introducing a new layer for sequence processing. The performance of this layer is studied and optimized in a line of papers. Theoretical foundations of state-space layers overlap with LSTMs and convolutional layers, in a sense containing them as special cases. It is demonstrated that the new layers can handle very long-range dependencies in sequences with over 10.000 tokens, while being much faster than transformers.