1 An overview of calibration
In practical applications, output vectors of probabilistic classifiers such as neural networks or random forests are always used for decision making in one way or another. Depending on the context of the decision, certain properties of these output vectors might be more relevant than others. For example, if the task at hand is purely a classification - say an input image needs to be labeled as frog, cat or human by the model - only the prediction, i.e. the $\operatorname{argmax}$ of the output vector plays a role. A slightly more demanding application of the same classifier would be to label an image as “unknown” if the confidence in the prediction is below a certain threshold. Then, not only the $\operatorname{argmax}$ but also the actual value of the maximal confidence is needed. Even more demanding decisions can require the entire confidence vector, for example the decision whether to turn the wheel of a car at high speed to avoid hitting something, at the cost of risking an accident. In such a situation, it is important to take all confidences into account. We might want our system to behave differently when there is a 40% chance that the recognized object is a human vs. a 40% chance of it being a cat, even if the prediction is “frog” with 60% confidence in both cases
For decision making as in the last two examples, it is important that confidence vectors are meaningful quantities. Ideally, we would like them to correspond to real probabilities in some sense - this is why we call the classifier probabilistic after all. Unfortunately, modern neural networks trained with gradient descent (but also other models like random forests), despite often being very accurate, tend not to output empirically valid probabilities. This phenomenon is often called “miscalibration of modern neural networks”.
As we will explain in the sections below, calibration is a topic with many nuances. While there is quite some active research, it is somehow underrepresented in the machine learning community. We believe that this is firstly because there are many situations in which only metrics related to accuracy matter, and secondly because even in situations in which calibration is very important, it is not entirely clear how to measure its effect. To remedy this and to bring measurements of calibration closer to the needs of practitioners, we propose an application-centric scheme for studying the effects of miscalibration in Sections 4 and 6. We also publish an open-source python library aimed at helping with all the topics related to calibration mentioned in this review, see [Pan21K].
1.1 Definition of strong calibration
A probabilistic classifier learns to predict confidences from inputs. For an input $x$, the output of the classifier is a confidence vector which we denote $c (x) = (c_{1} (x), \ldots, c_{K} (x))$, where $K$ is the number of classes. For our purposes, we can assume that $c$ is a deterministic function of $x$. In most of what follows, we will not be concerned with the input, so we will omit the dependency on it. This means that $c$ will typically denote the confidence vectors themselves and, sometimes, the classifier as a function mapping inputs to confidences; it should always be clear from the context what is meant by $c$. We assume that the confidences are always properly normalized, so that $\sum c_{k} = 1$.
Loosely speaking, we call a classifier calibrated if at test time the confidence vectors represent true probabilities, i.e. when for all $k \in \lbrace 1, \ldots, K \rbrace$:
\[ p_{\operatorname{observed}} (\operatorname{true}\operatorname{label}\operatorname{is}k \mid \operatorname{confidence}\operatorname{is}c) = c_{k} . \]
We can formulate this more rigorously as follows: Let $X, Y$ be random variables representing inputs and ground truth labels. The random variable $C := c (X)$ of confidence vectors takes values in the $(K - 1)$-dimensional simplex $\Delta^{K - 1}$. We are interested in the true probabilities of the ground truth labels given that a certain confidence has been observed, i.e. in the distribution of $Y \mid C$, which we will approximate using a test set. The vector of quantities $\mathbb{P} (Y = k|C)$, $k \in \lbrace 1 \ldots K \rbrace$ is a deterministic function of $C$: the canonical calibration function, $r : \Delta^{K - 1} \rightarrow \Delta^{K - 1}$, given by1 1 Here, and from now on, we use vector notation for class probabilities: when we write $Y$ we mean $Y = k$ for all $k$
\begin{equation} r (C) := \mathbb{P} (Y \mid C) . \label{can-calibration-definition}\tag{1} \end{equation}
When the distributions have densities, $r_{k} (c) = p (k \mid c)$, where $p (k|c)$ is the conditional density of $Y|C$. Because we will take expectations wrt. to $C$, we are only interested in the region of $\Delta^{K - 1}$ where $p (c) > 0$. Assuming that $(Y, C)$ has a density, the canonical calibration function is well defined everywhere in this set [Kle14P] (Ex.8.31). For this reason, in the sequel we will assume in computations that $p (y|c) = 0$ where $p (c) = 0$.
Note that, because $C$ is a random variable, $r \circ C$ is also a random variable. A probabilistic classifier $c$ is called strongly calibrated iff the canonical calibration function is the identity, i.e. iff
\begin{equation} c (X) = r (c (X)) . \label{strong-calibration}\tag{2} \end{equation}
Any metric that vanishes when $C$ and $r \circ C$ are equal almost surely, or equivalently when $r$ is the identity function almost everywhere, is thus a metric of strong calibration. In particular, the $L_{p}$ norms on the simplex (the range of $c (X)$) form such metrics, and we have the condition that $c$ is strongly calibrated iff
\[ | \operatorname{id}- r |_{p} = 0. \]
In general, accuracy and calibration are, to an extent, independent of each other.2 2 Although we will show that in many situations of practical relevance there are general relations between both A classifier can be perfectly accurate but not calibrated and perfectly calibrated but inaccurate. As an example for the former, think of a classifier that always predicts correctly but does so with a confidence of $1 / K + \varepsilon$ (where $\varepsilon$ is some small positive number). The accuracy is $1$ but clearly the classifier is under-confident, because being always correct means that $\mathbb{P} (Y = k|c (x)) = 1 \neq c_{k} (c) = 1 / K + \varepsilon$, and hence it is not calibrated. On the other side of the spectrum, a classifier which always predicts the (constant) population fractions is perfectly calibrated but generally inaccurate.
1.2 Why models are miscalibrated
Usually the objective on which a probabilistic classifier is trained is a so-called proper scoring rule [Lak17S], which for our purposes we can interpret to mean that the training objective reaches its optimum iff the confidence vectors outputted by the classifier are equal to the true conditional distribution of labels given inputs. Cross entropy and the so-called Brier score (the usual MSE between predictions and one-hot encoded labels) are proper scoring rules [Lak17S]. If the predictive distribution of a classifier parametrized by $\theta$ is denoted as $p_{\theta} (y \mid x)$, then a proper scoring rule is optimized at $\theta^{\ast}$ iff3 3 Once the classifier is fixed, the predictive probability $p_{\theta} (y \mid x)$ is the same as $c (x)$ in the previous section, i.e. $p_{\theta} (k \mid x) = c_{k} (x)$
\begin{equation} p_{\theta^{\ast}} (y \mid x) =\mathbb{P} (Y = y \mid x) \label{proper-scoring-rule}\tag{3} . \end{equation}
This means that if a classifier optimizes a proper scoring rule, it is both maximally accurate and perfectly calibrated. In this case, we say that $p_{\theta}$ is the best possible classifier.
Why, then, are modern neural networks often miscalibrated despite being trained on a proper scoring rule? The empirical observation is that they sacrifice calibration for accuracy, meaning that after a certain amount of training, the out-of-sample calibration begins to decline while the out-of-sample accuracy continues to improve. This was first noticed in [Guo17C] where several aspects of neural network miscalibration are explained in detail. There is however no solid theoretical understanding of why this happens, although experimentally, higher model capacity, batch normalization as well as low or no weight decay tend to reduce calibration.
Since the scoring rules measure calibration and accuracy simultaneously, miscalibration cannot be reliably captured by purely evaluating the training and validation losses (although in experiments one does see a decrease in calibration manifest itself as an increase in the test loss) and one has to resort to metrics that specifically target calibration.
1.3 Strong calibration and best possible post-processing
The optimality condition of a proper scoring rule is very similar to the condition for being strongly calibrated. Rewriting equation (3) in terms of random variables we get: a classifier $c$ optimizes a proper scoring rule iff (remember that we use vector notation for probabilities)
\begin{equation} c (X) =\mathbb{P} (Y \mid X) . \tag{4} \end{equation}
The only difference with respect to the definition of strong calibration is that we condition on $X$ instead of $c (X)$ on the right hand side. This is not a coincidence: Imagine that instead of samples from $X$ we observe samples from $g (X)$, for some $g$. Now we need a classifier taking $g (X)$ as input. The best possible classifier we could have, let us call it $c^{\star} \mid _{g}$, would optimize some proper scoring rule and fulfill
\[ c^{\star} \mid _{g} (g (X)) =\mathbb{P} (Y \mid g (X)) . \]
Setting now $g = c$, the original classifier, follows that reaching strong calibration for the original problem just means obtaining the best possible classifier given that one only observes $c (X)$ and not $X$ directly. We call this the best possible post-processing classifier and it fulfills:
\[ c^{\star} \mid _{c} (c (X)) =\mathbb{P} (Y|c (X)) = r (c (X)), \]
where $r$ is the canonical calibration function for $c$. We have then
\[ c^{\star} \mid _{c} = r, \]
and the immediate observation that any classifier $c$ that is already strongly calibrated cannot be improved through post-processing, where “improvement” means according to some metric of strong calibration, e.g. the $L_{p}$ norms mentioned above.
One property differentiating the analysis of calibration from classification after generic preprocessing is that by definition the inputs $c (X)$ to the function $r$ will live in the same space as the outputs, namely in $\Delta^{K - 1}$. Therefore, the canonical calibration function and approximations to it can be interpreted geometrically as simplex automorphisms.
Thus, optimizing calibration by post-processing the classifier’s output is equivalent to finding the overall best possible post-processing classifier, and the optimum is an approximation to the canonical calibration function $r$. One way of obtaining it is to fit a parametrized function using a proper scoring rule, which will often be the same loss used to train the original classifier.4 4 Alternative non-parametric methods estimate $r$ directly from the sample statistics. These tend to perform worse for large $K$, because of the difficulties involved in estimating probability distributions in high dimensions. For instance, the number of bins in typical binning schemes grows exponentially with the dimension The choice of this function is important, for it should counteract the tendency to over-fit in favor of accuracy described above. Stacking a neural network with the same tendency on top of another neural network is not helpful (although stacking a small NN on a random forest which was not trained on a proper score might work). Therefore, will need to resort to more restricted families of functions. The simplest example considers constant multiplications of the logits. Because these do not affect accuracy, a decrease in the post-processing training loss will be a reliable indicator of improved calibration. See Section 5.1 for details.
1.4 Other notions of calibration
Strong calibration is not the only useful calibration property one can define, although it is the most general one. Other notions of calibration can arise by conditioning on a function of $C$ instead of on $C$ itself. For example, by conditioning on the confidence in the predicted label, in a similar fashion as for the canonical calibration function (1) one can define the confidence calibration function $r_{\max} : [1 / K, 1] \rightarrow [0, 1]$ as
\[ r_{\max} (\max (C)) := \mathbb{P} (Y =\operatorname{argmax} (C) \mid \max (C)) . \]
As for strong calibration, one is only interested in $r_{\max}$ where it can be defined, i.e. where the density of $\max (C)$ is positive, and it is set to 0 everywhere else.
By conditioning on the confidence of a fixed label $k$, one arrives at the class-wise calibration function $r_{k} : [0, 1] \rightarrow [0, 1]$, with
\[ r_{k} (C_{k}) := \mathbb{P} (Y = k \mid C_{k}) . \]
The classifier is called confidence calibrated iff $r_{\max} =\operatorname{id}$ and classwise calibrated for class $k$ iff $r_{k} =\operatorname{id}$. Below we define calibration metrics inspired by these reduced notions. Both definitions are special cases of the concept of a calibration lens introduced in [Vai19E] which can be used to create calibration functions in a similar fashion. All such calibration functions are equal to the identity function if the strictly stronger condition of strong calibration holds.
The confidence and classwise calibration functions introduced above can be understood as canonical calibration functions of induced binary classifiers that predict two-dimensional confidence vectors as $(\max (C), 1 - \max (C)) \operatorname{and} (C_{k}, 1 - C_{k})$ respectively.5 5 The induced labels are then defined as $Y_{\operatorname{binary}} = \mathbb{1}_{\lbrace \operatorname{argmax} (C) \rbrace} (Y)$ or $Y_{\operatorname{cw}} = \mathbb{1}_{\lbrace k \rbrace} (Y)$ respectively From the discussion in Section 1.3 one can conclude that a confidence- or class-wise calibrated classifier is the best possible classifier that can be obtained by post-processing these induced classifiers.
2 Measuring calibration
Unlike metrics focused on the quality of predictions like accuracy, precision, or recall, there is no consensus about the best way to measure (or visualize) calibration. There are several reasons for that.
- Definition: $r (C)$ is a vector-valued quantity, as is $r (C) - C$. Depending on the situation at hand, different aspects of it are more relevant than others.
- Estimation: Typically, expressions involving $r (C)$, like expectation values, are difficult to estimate using a finite set. This is especially true for problems where the number of classes $K$ is large. As explained in Section 1.3, a good estimate of the canonical calibration function can be used to recalibrate the classifier, thus estimating $r$ directly is as hard as recalibrating.
- Optimality: While the commonly used losses are usually proper scoring rules and decreases in them over a test set can signalize better calibration, they generally do not vanish for strongly calibrated classifiers (nor do they vanish for the overall optimal classifier). Therefore, they are not proper measures of calibration.
- Comparison: Numerical values of miscalibration should be comparable across different data distributions, something that does not happen e.g. for loss functions. Unfortunately, most common calibration metrics, like those introduced below, do not have this property.
Finally, while a useful classifier always has to be accurate to some degree, calibration is often optional or even unnecessary. E.g. for applications like picking the most probable class or clustering that only require the predicted value (the $\operatorname{argmax}$), there might be no need to measure calibration at all.6 6 Nevertheless, one could argue the advantage of taking calibration into account for most decision problems using probabilistic classifiers This shows that in practical situations, measuring calibration should be done in a way that is useful for the problem at hand. We will elaborate on this in Section 4.
2.1 Calibration metrics and reliability curves
To overcome the difficulties outlined above, a scalar value representing miscalibration which vanishes when a classifier is strongly calibrated and an estimator for it.7 7 However, we will see examples which vanish without the classifier being strongly calibrated The latter is often defined through binning. Such scalar values are called calibration metrics. They necessarily obscure some properties of $r (C)$ that might be relevant for applications. Thus, in a decision making scenario it might be necessary to consider multiple calibration metrics or to create a custom one.
The simplest metrics are obtained focusing on the calibration either of a single class, or of the predictions. They also give rise to visualizations of miscalibration, as we explain below. The well known expected calibration error, ECE, stems from confidence calibration and is defined as follows. First introduce the one dimensional random variable $Z := \max (C)$, which we assume to have density $p (z)$. The ECE is computed by conditioning on $Z$ (as opposed to conditioning on the full confidence vector $C$ as above) as8 8 For the domain of integration, note that the maximum of a $K$-dimensional confidence vector is always larger or equal than $1 / K$, so $p (z) = 0$ for $z \not\in \left[ 1 / K, 1 \right]$
\begin{eqnarray*} \operatorname{ECE} & := & \mathbb{E}_{Z} (| \mathbb{P} (Y =\operatorname{argmax} (C) \mid Z) - Z |)\\\ & = & \int^1_{1 / K} p (z) | \mathbb{P} (Y =\operatorname{argmax} (C) \mid Z = z) - z | \mathrm{d} z. \end{eqnarray*}
The last equation also suggests a method to estimate the ECE by binning the one-dimensional domain of $Z$ and evaluating the empirical probabilities within the bins. The integral then turns into a sum over the bins.
Note that the ECE is zero only if $| \mathbb{P} (Y =\operatorname{argmax} (C) \mid Z = z) - z |$ vanishes a.s. wrt. $Z$. This function can be conveniently visualized by plotting $z$ on one axis and $\mathbb{P} (Y =\operatorname{argmax} (C) \mid Z = z)$ on the other. The resulting graph is called reliability curve. For a confidence calibrated classifier (and hence for a strongly calibrated one too), the reliability curve is exactly diagonal. Note that such a visualization can be misleading since it does not take into account $p (z)$, which for a binning scheme is approximated by the fractions of data points per bin and can be thought of as weights. The reliability curve might be far from the diagonal in some bins but the ECE could still be small if the population fractions in these bins are low. The intuition here is that the reliability curve just shows how miscalibrated a prediction is for all possible confidences while the ECE also takes into account how often such confidences are actually returned by the classifier.
Similarly, instead of focusing on the predictions we can calculate class-wise
calibration errors and reliability curves for selected classes. Let $p
(c_{k})$ stand for the marginal probability density of the 1-dim. random
variable $C_{k} = c_{k} (X)$ - the confidence of class $k$.9
9 Here, contrary to the
density for the predicted class, $p (c_{k})$ is defined on the whole interval
$[0, 1]$ We can define the class-wise expected
calibration error $\operatorname{cwECE}_{k}$ as
\begin{eqnarray*} \operatorname{cwECE}_{k} & := & \mathbb{E}_{C_{k}} (| \mathbb{P} (Y = k \mid C_{k}) - C_{k} |)\\\ & = & \int^1_{0} p (c_{k}) | p (k \mid c_{k}) - c_{k} | \mathrm{d} c_{k},\\\ \operatorname{cwEC} \mathrm{E} & := & \frac{1}{K} \sum_{k} \operatorname{cwECE}_{k} . \end{eqnarray*}
Again, one can estimate this with binning and visualize $| \mathbb{P} (Y = k \mid C_{k} = c_{k}) - c_{k} |$ using reliability curves. These approximate the reduced calibration functions defined in Section 1.4.
Note that conditioning on the prediction $Z$ or a single confidence $C_{k}$ is not the same as conditioning on the full vector, even after taking the expectation values. In other words, in general (note that the expectations are taken wrt. $C$):
\begin{eqnarray*} \operatorname{cwECE}_{k} & \neq & \mathbb{E}_{C} (| r_{k} (C) - C_{k} |),\\\ \operatorname{ECE} & \neq & \mathbb{E}_{C} (| P (Y =\operatorname{argmax} (C) \mid C) - \max (C) |) . \end{eqnarray*}
In fact, a classifier might have all class-wise calibration errors equal to zero (and also ECE being zero) but still not be strongly calibrated! See [Vai19E] for an example. There has been effort to design metrics which are better at capturing strong calibration and to devise statistical tests for strong calibration [Wid19C, Vai19E]. However, demanding strong calibration might be too much to ask for specific applications, where only certain aspects of calibration may matter.
The methods outlined above demonstrate that there is no single one-fits-all solution for measuring calibration. The commonly used metrics always obscure some aspect of calibration and the full strong calibration is difficult to evaluate and may be not needed.
3 Computing and visualizing miscalibration
We now elaborate on the computation of calibration metrics and reliability curves using a finite data set $D$. We will focus on the ECE but the same considerations apply to cwECE and similar metrics.
3.1 Estimating naively with binning
The most straightforward way of estimating the ECE is with a constant binning scheme: Let $P := \left\lbrace b_{0} = \frac{1}{K}, \ldots, b_{N} \right\rbrace$ be a uniform partition of the interval $[1 / K, 1]$ in $N$ bins $I_{j} = [b_{j - 1}, b_{j})$, with $I_{N} = [b_{N - 1}, b_{N}]$. The corresponding estimator $\widehat{\operatorname{ECE}}_{P ; D}$ takes the form
\[ \widehat{\operatorname{ECE}}_{P ; D} = \sum_{m = 1}^N \frac{N_{m}}{| D |} | \operatorname{acc}_{m ; D} -\operatorname{conf}_{m ; D} |, \]
where $N_{m}$ is the number of samples in bin $m$, and, letting $Z = \max (C)$ as above,
\[ \operatorname{acc}_{m ; D} := \hat{\mathbb{P}}_{D} (Y =\operatorname{argmax} (C) \mid Z \in I_{m}), \]
\[ \operatorname{conf}_{m ; D} := \hat{\mathbb{E}}_{D} (Z \mid Z \in I_{m}) \approx \frac{b_{m} + b_{m + 1}}{2}, \]
are the empirical accuracy and average confidence in the bins respectively, and $\hat{\mathbb{P}}_{D}, \hat{\mathbb{E}}_{D}$ stand for the usual (counting) sample estimators of $\mathbb{P}, \mathbb{E}$ over the set $D$. We explicitly highlight the dependence on the dataset $D$ in all relevant quantities.
With such a binning scheme we can immediately create a reliability curve by
plotting the accuracies against the confidences (or simply against the centers
of the bins), see Figure 1. If the classifier is
confidence calibrated and the estimates of $\operatorname{acc}_{m}$ are good
enough (which depends on the number of samples in the bin), the reliability
curve will be almost diagonal.
Figure 1.
Prediction reliability curve of
a small MLP trained on a synthetic data set. In the middle we see large
deviations from the diagonal
Unfortunately, a lot of important information is hidden in this kind of visualization. In particular, the weight factors $N_{m} / | D |$ are not displayed. In other words, each bin contributes equally to the plot, independently of how many samples fall into it. This information can be added with a histogram of the confidences, as shown in Figure 1.
3.2 Other binning schemes
Estimators based on a fixed number of equally sized bins, despite being simple to implement and intuitively clear, have multiple downsides. One of them is the previously mentioned loss of information in the resulting reliability curve. Another one is that they may have a significant bias, depending on the distribution from which $D$ was sampled. Examples showing this bias were constructed in [Vai19E].
Generally, the estimate of the ECE will heavily depend on the binning scheme,
especially when $D$ is small. Several binning schemes that are adapted to the
data have been proposed in the last years, for example in [Nix20M] and [Din20R]. If in such an adaptive scheme the bins have an
equal number of samples, the resulting reliability curve is easier to interpret
and there is no need to plot the bin populations as done above.
Figure 2. Same curve as in
Figure 1 but with an added histogram of
confidences. We see that most of the bins in the middle are almost empty (in
comparison) and hence don’t contribute much to the
ECE
3.3 A note on variance and convergence
Since randomness is involved in the selection of test sets, an analysis of variance and convergence rate of the estimators is required to make statistically significant statements. Several methods for such an analysis are based on the idea of consistency resampling [Bro07I], where one assumes that the classifier is strongly calibrated and samples new labels (not real ground truth labels) from categorical distributions constructed from the classifier’s outputs. Repeating this procedure multiple times allows to compute confidence intervals for the per-bin accuracies and hence to assess whether the observed value of the estimator or the observed reliability curves are consistent with strong calibration.
While there is a lot more that must be said about the statistical properties of calibration metrics, it is beyond the scope of this introductory review.
4 Measuring calibration through simulation
Even if one has an application in which calibration does play a role, it might still not be clear how relevant it is for an accurate classifier. In other words, given a classifier that predicts correctly in, say, 90% of the cases, how important is it for the application that this classifier is also calibrated and which calibration metrics are the relevant ones?
One way to evaluate this is to identify the quantity one wishes to optimize and to analyze the effect of miscalibration of the classifier while maintaining accuracy. This quantity may be the expected gain in value in a financial application, where a mixed strategy based on predicted confidences is applied, or the expected percentage of successful treatments in a medical application, based on confidences in the diagnosis.10 10 appliedAI has developed KALE, the calibration game, to illustrate this situation in an idealized problem of resource management in healthcare The confidence-based decision process can then be simulated and probabilistic classifiers can be compared to each other directly in an application-centric context.
There are two fundamentally different situations in which this procedure can be useful: requirements engineering and model evaluation. Let us view these situations through the eyes of a product owner (PO) who is to assign the task of developing a probabilistic classifier to a team of experts. The PO needs to specify in advance how well the classifier must perform to be acceptable (including calibration), and she also needs a method to evaluate the classifier on a test set. A simulated decision process helps in both situations.
Requirements engineering with fake classifiers. At this stage there is no model yet and the goal is to understand the minimal requirements on the model quality needed to reach the application’s target performance. Having the simulated decision making process at hand, one could use a fake classifier, i.e. a generator of confidence vectors and ground truth labels that is not based on actual data (and does not even take input), but has adjustable accuracy and calibration. Using such fake classifiers one could simply compute how sensitive the quality of decision making is to accuracy and calibration without actually training any models. This is a cheap and efficient method of finding out which properties of calibration matter in the specific context of interest. We say more about such fake classifiers in Section 6.
Model evaluation on test sets. Once classifiers have been trained, accuracy and calibration metrics can be computed on test sets. As mentioned before, it is often far from trivial to interpret the various calibration errors when one is concerned with performance in a specific context. Instead, one could evaluate models using the same simulated decision process as for requirements engineering, running it on the test set with the real classifier.
5 Recalibrating
The calibration of a classifier can be improved either by adjusting the training or modeling, or by recalibrating via post-processing using a heldout set. Examples of the former include training an ensemble of models [Lak17S] or using specialized loss functions [Muk20C].
Here we focus on the second approach, i.e. recalibrating with a held-out set. The practical advantage of these methods is that they can be applied to any classifier and, by definition, do not require re-training. Since the classifier itself is not modified in this approach, we can forget about the actual inputs and directly consider the distribution of confidence vectors obtained on the test set. We are thus concerned with the problem of having samples of true labels and confidences, following a miscalibrated distribution $Y, C$ with $C := c (X)$, and want to find a calibration function $r_{\theta} : \Delta^{K - 1} \rightarrow \Delta^{K - 1}$ such that $Y|r_{\theta} (C)$ is better calibrated (see Section 1.3 for more details). Note that, as long as one ensures that for every $c \in \Delta^{K - 1}$ it holds that
\[ \operatorname{argmax} (r_{\theta} (c)) =\operatorname{argmax} (c), \]
then mapping the output confidences with $r_{\theta}$ does not have an effect on the model’s accuracy.
There are a number of different methods, parametric and non-parametric, for constructing or learning calibration functions. We will only highlight two here: temperature scaling and an extension thereof called Dirichlet calibration. For a summary of other techniques, see [Guo17C, Kul19T].
5.1 Temperature scaling
Temperature scaling was first applied to multi-class problems in [Guo17C]. For concreteness, consider a standard neural network classifier. The idea and implementation are fairly straightforward: scale the output logits of the network with a learned parameter prior to applying the softmax. The parameter is expressed as $1 / T$ and $T$ is called temperature due to analogies in statistical physics. T can be learned by minimizing the negative log likelihood (NLL) over the held-out set. Note that scaling the logits uniformly does not alter the ranking of predictions, thus accuracy is unaffected by it. Temperature scaling proposes a calibration function of the form:
\[ r_{T} (c) = \sigma \left( \frac{\log (c)}{T} \right), \]
where the logarithm acts component-wise and $\sigma$ is the $\operatorname{softmax}$ function, although in implementations the scaling should rather act directly on the predictor’s logits, before the application of the softmax that converted them to confidences.
Temperature scaling has been empirically shown to be efficient in reducing the ECE of neural networks. Unfortunately, it may under-perform in improving overall calibration, e.g. in reducing class-wise calibration errors. This is where Dirichlet calibration is reported to perform better
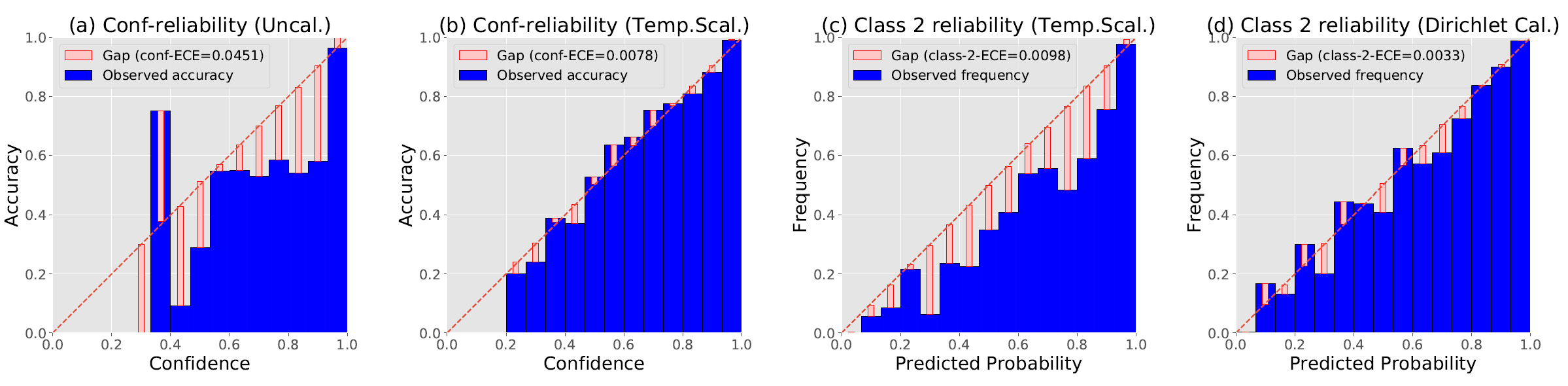
Figure 3. Reliability diagrams of c10\_resnet\_wide32 on CIFAR-10: (a)
confidence-reliability before calibration; (b) confidence-reliability after
temperature scaling; (c) classwise-reliability for class 2 after temperature
scaling; (d) classwise-reliability for class 2 after Dirichlet calibration.
Image and description taken from [Kul19T]
5.2 Dirichlet calibration
A straightforward extension of temperature scaling is to multiply the logits by a weight matrix $W \in \mathbb{R}^{K \times K}$ and to add a bias vector $b \in \mathbb{R}^K$. In other words, this extension assumes a calibration function of the form
\begin{equation} r_{W, b} (c) = \sigma (W \cdot \log (c) + b) . \label{dirichlet-calibration}\tag{5} \end{equation}
Again, in implementations one should use logits instead of taking the log of $C$, in which case the procedure is also known as matrix scaling (theoretically, the two are equivalent but in practice matrix scaling performs slightly better, presumably due to rounding errors when calculating log of softmax of logits). Equation (5) can be shown to follow from the assumption that confidences conditioned on ground truth are distributed with Dirichlet distributions, i.e. that there are $K$ vectors with positive entries $\alpha^{(k)} = (\alpha _{1}^{(k)}, \ldots, \alpha _{K}^{(k)})$ such that for each $k \in \lbrace 1, \ldots, K \rbrace$:
\[ C \mid Y = k \quad \sim \quad \operatorname{Dir} (\alpha^{(k)}), \]
hence the name, Dirichlet calibration. This recalibration scheme has two downsides: it can easily overfit due to the number of parameters (quadratic in number of classes) and it does not preserve ranking and accuracy of predictions. The latter might actually not be a problem as recalibration also has the potential to increase accuracy, especially if trained to optimize NLL. However, one needs to be more careful if using a different objective.
In the initial experiments with matrix scaling in [Guo17C] the authors encountered severe overfitting, even with regularization. However, with a recently proposed regularization scheme that separately regularizes off-diagonal elements of $W$ and the intercept $b$ (giving rise to the name ODIR - off-diagonal and intercept regularization), matrix scaling outperformed temperature scaling in most cases with up to 100 classes (see [Kul19T] for details). Importantly, it improved calibration not only as measured by ECE but also by class-wise calibration errors - where temperature scaling performed significantly worse.
6 Fake classifiers
We have mentioned that for requirements engineering it may be useful to create fake confidence vectors and ground truth labels that have a pre-determined accuracy and calibration. By fake we mean that instead of being computed by applying a classifier to data, the confidences and labels are simply sampled from a distribution.
Such fake classifiers are also useful for the evaluation of tools in calibration, like metrics and recalibration algorithms. For metrics, one can empirically study convergence rates since, typically, for a fake classifier the true value of a calibration metric is a known integral. Recalibration algorithms can be benchmarked with fake classifiers. This is important since miscalibration can arise in a number of different ways: classifiers can be overconfident or under-confident in predictions, be overconfident for some classes and under-confident for others or have a mixture of different behaviors. To the best of our knowledge, recalibration algorithms have been studied up to now by applying them to models like deep neural networks trained on selected data sets, like CIFAR, MNIST and ImageNet. Fake classifiers enable the analysis of recalibration for a much more diverse variety of scenarios, and in a controlled way.
However, creating fake classifiers where accuracy and calibration can be adjusted mostly independently of each other is not entirely trivial. This construction is explained in detail in [Pan22C] where the results of benchmarking several algorithms and metrics will be presented as well. Accompanying the paper, we will open-source the code for creating fake classifiers and performing benchmarking as part of the aforementioned library [Pan21K] containing general tools for calibration.
7 Accuracy and calibration
We already mentioned that accuracy and calibration are up to a point independent from each other. However, for an important special case, there is a relation between accuracy and ECE. This case is that of always overconfident or under-confident classifiers.11 11 “Always” means that the confidence $c^{\ast} = \max (c (x))$ of every prediction $y =\operatorname{argmax}c (x)$ is greater than, resp. lower than, the value $\mathbb{P} (Y = y|c (X) = c^{\ast})$ Since modern neural networks tend to be always overconfident and ECE is one of the most widely used calibration metrics, this relation is of practical importance. In [Pan22C], we prove:
Lemma 1:
For always overconfident classifiers, it holds that:
\[ \operatorname{ECE} \leq 1 -\operatorname{acc}. \]
For always underconfident classifiers, it holds that:
\[ \operatorname{ECE} \leq \operatorname{acc}. \]
While the second inequality is not very interesting (for an accurate classifier it is a very loose bound), the first one is tighter and makes intuitive sense: an overconfident classifier that is very accurate simply does not have much room for miscalibration. In fact, a perfectly accurate classifier cannot be overconfident at all - at perfect calibration it will always predict confidence vectors with $1$ at the predicted class and $0$ everywhere else. This inequality holds for many neural networks and shows that it might be enough to only improve accuracy - the ECE will be automatically small when the accuracy is very high. For requirements engineering in situations where the ECE is a relevant metric, this bound should be taken into consideration.